召回09：双塔模型+自监督学习

本博文引自王树森老师推荐系统。
视频地址：召回09：双塔模型+自监督学习_哔哩哔哩_bilibili
课件地址： https://github.com/wangshusen/RecommenderSystem

大家好，我是王树森，前几节课详细讲解了双塔模型，这节课介绍一种改进双塔模型的方法，叫做自监督学习，用在双塔模型上会提升业务指标。

本节简介

这是双塔模型，左边是用户塔，右边是物品塔，自监督学习的目的是把物品塔训练得更好。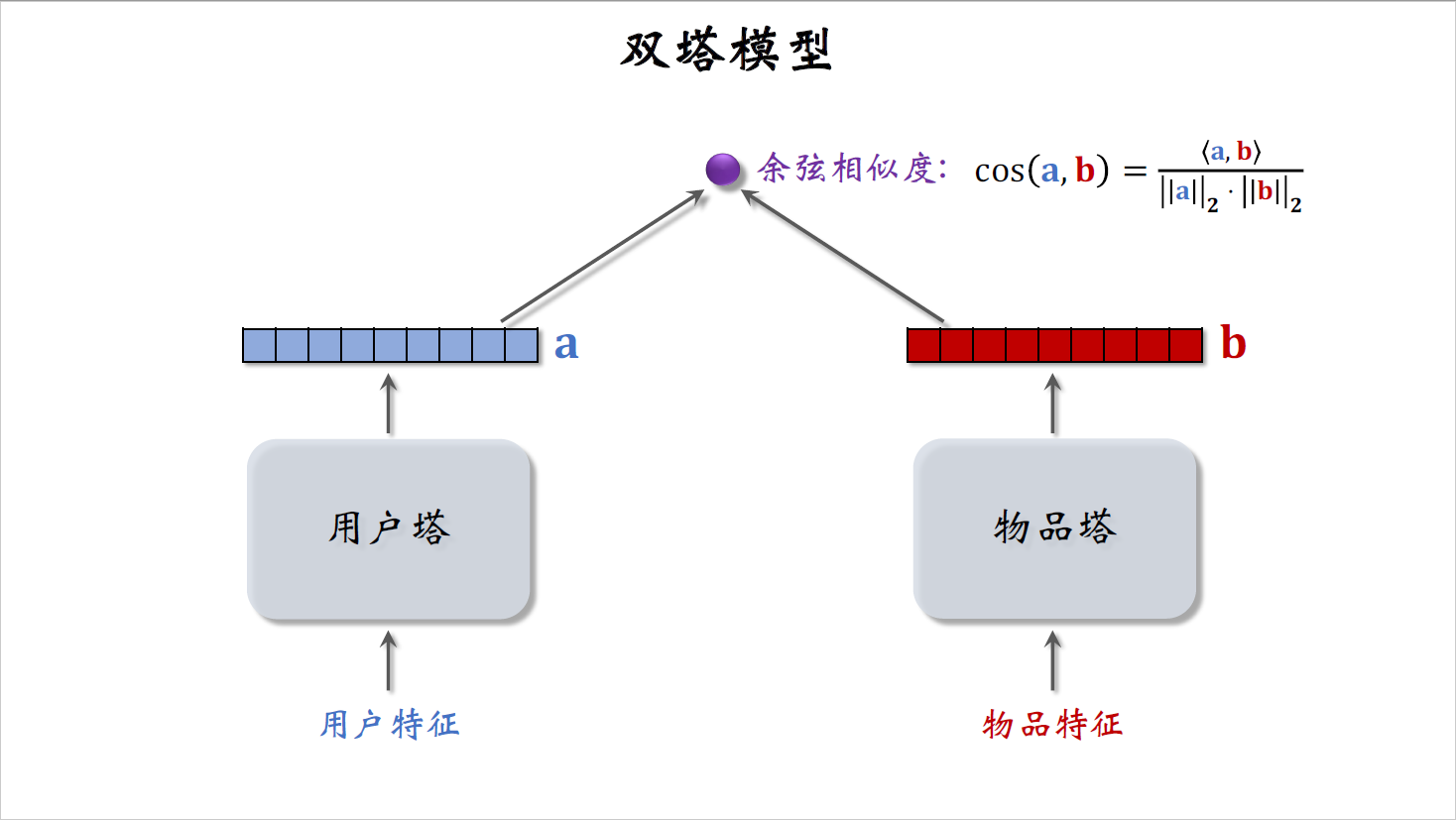

为什么要做自监督学习呢？在实际的推荐系统中，数据上的问题会影响双塔模型的表现，实际推荐系统都有头部效应：少部分的物品占据了大部分的点击，而大部分的物品点击次数都不高。训练双塔模型的时候，用点击数据作为正样本，模型学习物品的表征，靠的就是点击行为。如果一个物品给几千个用户曝光，有好几百个用户点击，那么物品的表征就会学的比较好。反过来，长尾物品的表征学的就不够好，这是因为长尾物品的曝光和点击次数太少，训练的样本数量不够。
一种比较好的解决方法是自监督学习，对物品做data augmentation，这样的话可以更好地学习长尾物品的向量表征。这节课介绍的方法来自于google在2021年发表的论文，这篇论文很靠谱，大家公认复现这篇论文能落地拿到收益。

复习listwise训练

在开始这节课内容之前，我们先复习一下双塔模型的训练。
双塔模型做listwise训练，用batch内负样本。在这个图中，左边是用户，右边是物品，中间的箭头表示用户点击过物品，图中任意一对样本都是正样本，比方说第二个用户点击过第二个物品，这就说明用户对物品感兴趣，这个二元组是一对正样本。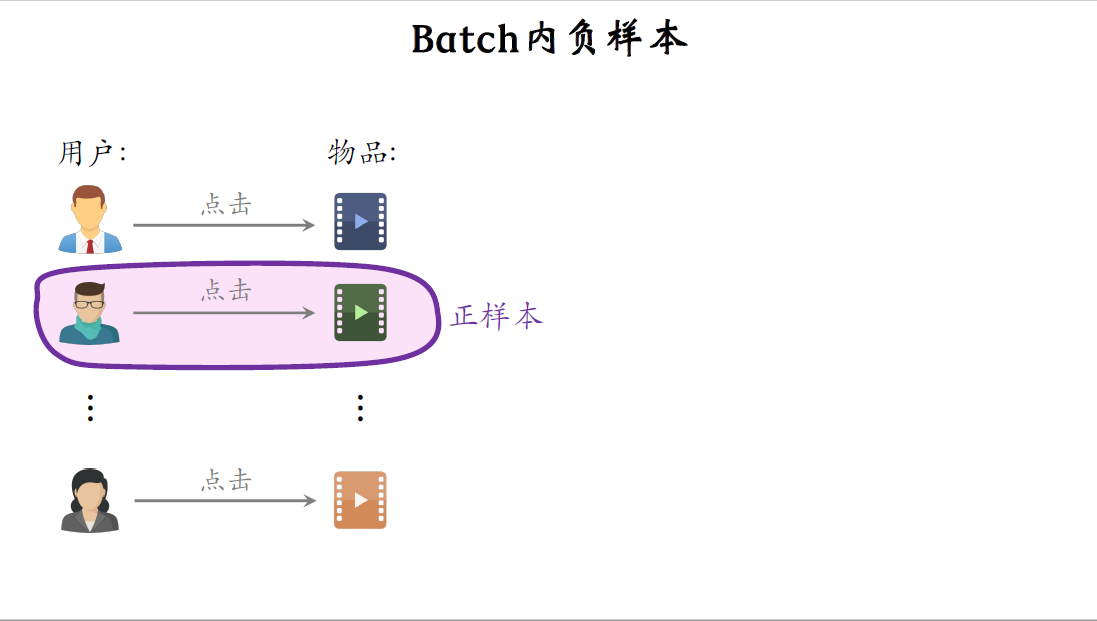

前面的课讲过batch内负样本是什么意思，举个例子，第一个用户跟第二个物品可以组成一对负样本，第一个用户跟第三个物品，也可以组成一对负样本。设一个batch内一共有$n$对正样本，这$n$对正样本可以组成$n$个list，每个list中有一对正样本和$n-1$对负样本。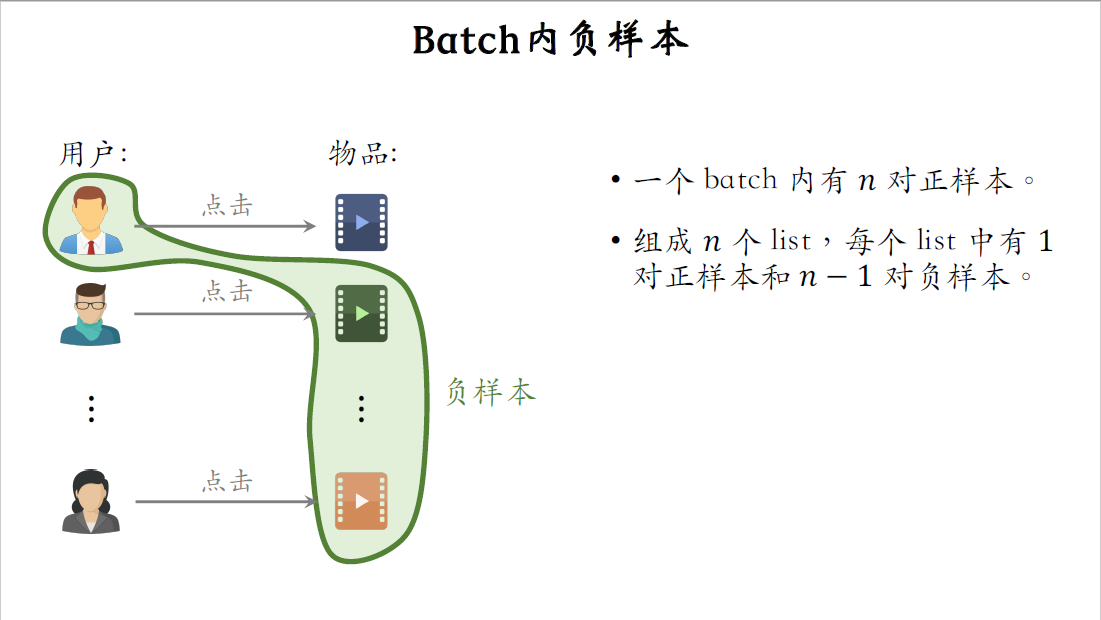

刚才说了，做训练的时候，每次要随机抽一个batch的数据，包含$n$对正样本，每对正样本包含一个用户和一个物品，用户点击过物品。用户塔把用户表征为向量$a$，物品塔把物品表征为向量$b$，把$n$对正样本记作$(a_1,b_1)$，$(a_2,b_2)$，一直到$(a_n,b_n)$。
再看一下负样本，$(a_i,b_j)$这样的二元组都是负样本，$i$和$j$不相等，第$i$个用户大概率会对第$j$个物品不感兴趣，所以是一对负样本。做训练的时候，要鼓励$\cos {(a_i,b_i)}$尽量大，$\cos {(a_i,b_j)}$尽量小，也就是说要让模型给正样本打的分数尽量高，给负样本打的分数尽量低。

损失函数

下面推导损失函数，这里考虑batch内第$i$个用户和全部$n$个物品。这$n$个数值分别是$\cos(a_i,b_1)$，$\cos(a_i,b_2)$，到$\cos(a_i,b_n)$，把这$n$个数值输入softmax激活函数，得到$n$个概率值记作$p_{i,1}$到$p_{i,n}$ 。
看一下这里$a_i$和$b_i$组成一对正样本，如果双塔模型的预估足够准确，那么$\cos(a_i,b_i)$应该比其他$n-1$个cos相似度大很多，softmax输出的概率值$p_{i,i}$应该接近一，把这$n$个概率值记作向量$p_i$。
上面的$n$个数值是标签，全都是零，只有这个是一，它对应正样本。把这$n$个标签记作向量$y_i$。$y_i$只有第$i$个元素是一，其余元素都是零。做训练的时候，我们希望向量$p_i$尽量接近向量$y_i$ 。$p_i$越接近$y_i$，说明双塔模型的预估越准确。
用$y_i$和$p_i$的交叉熵作为损失函数，其实就等于$-\log p_{i,i}$，把$p_{i,i}$替换成softmax函数输出的第$i$个数值，那么就得到这一项，感兴趣的函数话可以自己推导一下，我就不具体讲了。这就是listwise训练双塔模型的损失函数，训练的时候要最小化损失函数。

纠偏

前面正负样本的课程中讲过，batch内负样本会过度打压热门物品造成偏差，如果用batch内负样本，就需要做纠偏，这里再回顾一下。
我们把物品$j$被抽到的概率记作$p_j$，它正比于物品$j$的点击次数，反映出物品的热门程度。双塔模型用向量$a_i$和$b_j$的余弦相似度，作为用户$i$对物品$j$兴趣的预估。做训练的时候，要把$\cos(a_i,b_j)$替换成$\cos(a_i,b_j) -\log{p_j}$，这样起到纠偏的作用，热门物品不至于被过分打压。训练结束之后，在线上做召回的时候，还是用原本的余弦相似度$\cos(a_i,b_j)$，线上召回的时候不用做这种调整，不用减掉$\log{p_j}$。
这种纠偏的方法是下面这篇论文提出的，感兴趣的话可以自己读一下。

训练双塔模型

训练双塔模型每次要用一个batch的样本，从点击数据中随机抽取$n$个用户物品二元组，组成一个batch。这是我们刚才定义的损失函数，把损失函数记作$L_{main} [i]$，它对应batch内第$i$个用户。双塔模型的预测越准，这个损失函数越小。训练双塔模型的时候要做梯度下降，减小损失函数。损失函数是$n$项的平均，序号$i$指的是第$i$个用户，$n$的意思是batch中一共有$n$个用户。

自监督学习

刚才回顾了双塔模型的listwise训练方式，同时训练用户塔和物品塔，接下来我们用自监督学习训练物品塔。
下面是两个不同的物品，记作$i$和$j$。对两个物品的特征做随机变换，得到特征$i^\prime$和$j^\prime$，对两个物品做另一种特征变换得到特征$i^{\prime\prime}$和$j^{\prime\prime}$。把这些变换过的特征输入物品塔，模型一共只有一个物品塔，这里画的四个物品塔指的是同一个，他们都用相同的参数。物品塔输出的这两个向量记作$b_i^{\prime}$和$b_i^{\prime\prime}$，它们都是物品$i$的向量表征，但是由于下面的随机特征变换，导致两个向量不完全相等。
两个向量是同一个物品的表征，如果物品塔足够好，两个向量应该有很高的相似度，训练的时候会鼓励两个向量的cos相似度尽量大。
右边两个物品塔输出的向量，叫做$b_j^{\prime}$和$b_j^{\prime\prime}$，它们都是物品$j$的向量表征。同样的道理，两个向量应该有比较高的相似度。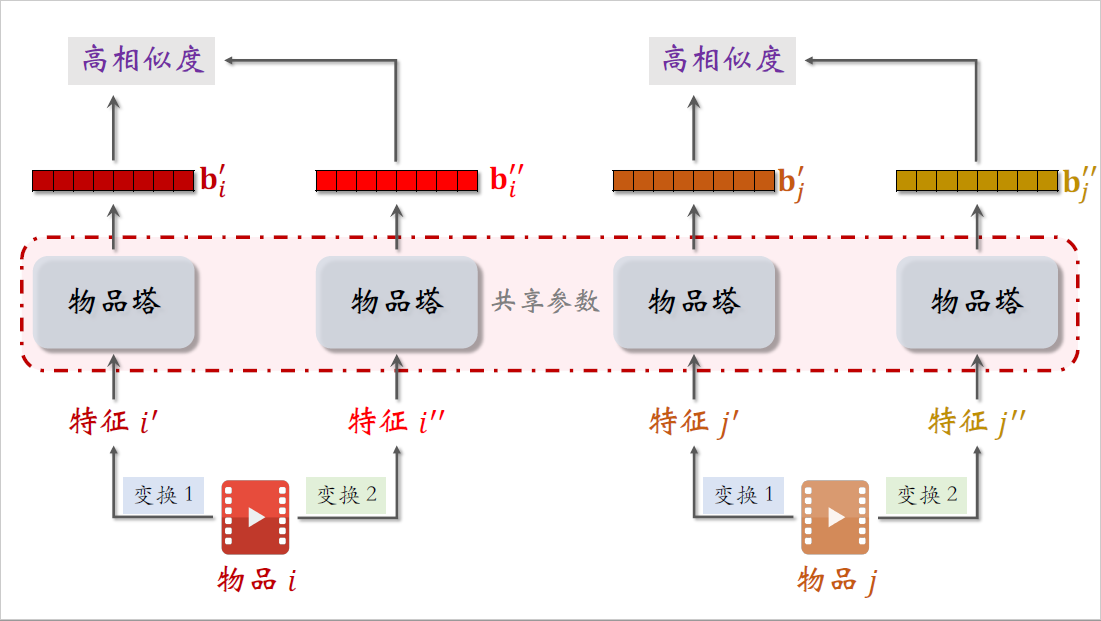

但是不同的物品的向量表征应该离得尽量远，也就是说这些向量的分布应该尽量spread out，分散开，而不是集中在一小块区域。向量$b_j^{\prime}$和$b_j^{\prime}$对应两个不同的物品，它们的相似度应该比较低才对。做训练的时候，应该降低$b_j^{\prime}$和$b_j^{\prime}$的cos相似度，同样的道理，$b_j^{\prime\prime}$也应该跟物品$i$的向量有低相似度。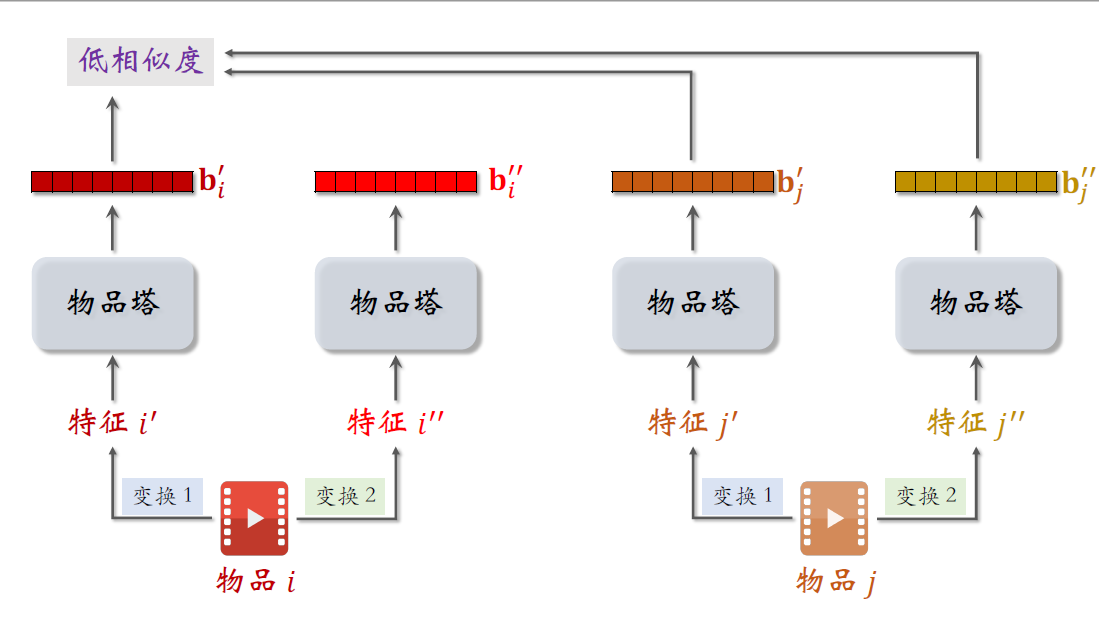

概括一下，自监督学习的目标是让物品$i$的两个向量，$b_j^{\prime}$和$b_i^{\prime\prime}$有较高的相似度，尽管这两个向量对应不同的特征变化，而物品$i$和物品$j$的向量，$b_i^{\prime}$和$b_j^{\prime\prime}$应该有较低的相似度。训练的时候，要鼓励相同物品的两个向量，有尽量大的余弦相似度，而不同物品的向量有尽量小的余弦相似度。

自监督学习应用到很多种特征变换，我挨个解释：

Random Mask

第一种是random mask，随机选出一些离散特征，把它们遮住。比方说选出类目这个特征，举个例子，某物品的类目特征是数码和摄影，一个物品可以有多个类目，如果不做random mask，正常的特征处理方法是，对数码和摄影分别做embedding，得到两个向量，再取加和或者平均，最终输出一个向量，表征物品的类目。如果对类目特征做mask，这物品的类目特征就变成了default，意思是默认的缺失值，然后对defaults做embedding，得到一个向量表征类目，也就是说做mask之后，物品的类目特征直接被丢掉，数码和摄影都没了。

Dropout

第二种特征变换是Dropout，仅对多值的离散特征生效。
多指离散特征是什么意思呢？举个例子，类目是一个离散特征，而且一个物品可以有多个类目，比如同时包括美妆和摄影这两个类目。Dropout意思是随机丢弃特征中50%的值，举个例子，某物品的类目包括美妆和摄影，做Dropout随机丢弃50%的值，碰巧把摄影给丢掉了，那么该物品的类目只包括美妆这一个值，请注意Random Mask和Dropout的区别，mask意思是把整个类目特征都丢掉，把美妆和摄影这两个值都不要了，而Dropout只丢掉摄影这一个值，还保留美妆这个值。

互补特征

前面讲了random mask和Dropout，第三种特征变换是互补特征，Complementary。
举个例子，假设物品一共有四种特征，包括ID、类目、关键词、城市，正常的做法是，把这四种特征的值分别做embedding，然后拼起来输入物品塔，最终得到物品的向量表征。
互补特征，意思是把特征随机分成两组，比如ID和关键词一组，类目和城市作为另一组，对于第一组保留ID和关键词，把另外两个特征mask掉，也就是替换成default，物品塔把这第一组特征作为输入，然后输出一个向量作为物品的表征，对于第二组保留类目和城市，把其他两个特征替换成default，把这些特征输入品塔得到另一个向量，也是对这个物品的表征。由于是对同一个物品的表征，这两个向量应该有比较高的相似度，训练的时候要鼓励cos相似度尽量大。

Mask一组关联特征

前面介绍了三种特征变换的方法，第四种是最复杂的，要随机遮住一组关联的特征。
之所以用这种方法，是因为特征之间有较强的关联，遮住一个特征并不会损失太多的信息，模型可以从其他强关联特征中学到遮住的特征，最好是把关联的特征一次全都遮住。举个例子，物品的受众性别是一种特征，特征的取值记作集合$U$，包含男性、女性、中性，物品类目是另一种特征，特征的取值记作集合$V$，包含美妆、数码、足球、摄影、科技等100多个取值。物品的受众性别和类目之间不是独立的，而是存在某种关联。比方说受众性别取值为小$u$等于女性，类目取值为小$v$等于美妆，这两个值同时出现的概率，$p(u,v)$比较大，$p(u,v)$意思是受众性别为女性，类目为美妆，两者同时出现的概率。再举个例子，物品受众性别为女性，而类目为数码，这个概率$p(u,v)$就比较小，很显然数码类的物品受众性别普遍为男性，而不是女性。假如我们知道类目是美妆，那么受众性别大概率是女性；假如我们知道类目是数码，那么我们知道受众性别大概率是男性。我用这个例子说明特征之间存在关联，比如类目和受众性别的关联就很强。

设$p(u)$为某特征取值为$u$的概率.以受众性别为例，有20%的物品受众性别为男性，30%的物品受众性别为女性，50%的物品受众性别为中性。

一个特征取值为$u$，另一个特征取值为$v$，同时发生的概率记作$p(u,v)$，比方说一个物品的受众性别是女性，而类目是美妆，这个概率等于3%，再比方说物品的受众性别是女性，而类目是数码，这个概率等于0.1%。

我们离线计算特征两两之间的关联，具体用mutual information来衡量两个特征关联越强，他们的mutual information就越大，用$MI(U,V)$表示特征$U$和$V$的mutual information。
我不具体解释mutual information的定义了，大家只需要知道两种特征的关联强，那么$p(u,v)$就比较大，两种特征的mutual information就比较大。这就是用mutual information的原因，它可以衡量两个特征的关联有多强。

特征变换的目标是mask1组关联的特征，具体这样实现：设一共有k种特征，要离线计算特征两两之间的mutual information，得到一个k乘以k的矩阵，表示特征之间的关联。每次随机选一个特征作为种子，比如选中了类目特征，然后从全体k种特征中找到种子最相关的，$\frac{k}{2}$种特征，比方说类目特征是种子，那么关键词和受众性别都属于关联的特征。把种子特征以及相关的$\frac{k}{2}$种特征，都做mask，比方说类目关键词，受众性别都是强关联的特征，把它们都遮住，保留其余的$\frac{k}{2}$种特征。

Mask关联特征的好处是实验效果好，推荐的主要指标比其他几种特征变换要好一点。Mark关联特征的坏处是很复杂，实现难度大，需要计算特征之间的mutual information，而且以后也不太好维护，每添加一个新的特征都需要重新算一遍所有特征的mutual information，在工业界通常会考虑投入产出比，为了指标再高一点，花更多的时间做开发以后还不好维护，可能不太划算。

概括一下，前面一共讨论了四种特征变换的方法，分别是random mask，Dropout，互补特征，还有mask1组关联的特征。这其中任何一种特征变换都可以。

训练模型

刚才讲了如何变换物品的特征，接下来具体讲如何用变换后的特征训练模型，要从全体物品中做随机抽样，得到M个物品，作为一个batch，冷门物品和热门物品被抽样到的概率是相同的。
注意跟训练双塔的区别，训练双塔用的数据是根据点击行为抽样的，热门物品被抽到的概率大。
均匀抽样到M个物品之后，对物品特征做变换，要用两种不同的特征变换，每个物品被表征为两个向量，这是第$i$个物品的损失函数，记作$L_{self}[i]$。

下面我要解释损失函数是怎么样推导出来的，这里考虑batch中第$i$个物品的特征向量$b_i^{\prime}$，还有全部$m$个物品的特征向量$b^{\prime\prime}$。这$m$个数值是第$i$个物品和所有$m$个物品的cos相似度，把这$m$个数值输入softmax激活函数，得到$m$个概率值，记作$S_{i,1}$、$S_{i,2}$到$S_{i,m}$，这里对应的是一组正样本$b_j^{\prime}$和$b_i^{\prime\prime}$，这两个向量都是对物品$i$的表征，只不过做了不同的特征变换，导致两个向量不相等，如果物品塔足够好，那么两个向量的cos相似度应该很高。
其余$m-1$个数值都对应负样本，两个向量属于不同的物品，它们的cos相似度应该比较小，所以softmax输出的概率值$S_{i,i}$应该接近一，其余$m-1$概率值应该接近零。
把这$m$个概率值记作向量$s_i$，上面的$m$个数值是标签全都是零，只有这个是一，它对应正样本，把这$m$个标签记作向量$y_i$，$y_i$只有第$i$个元素是一，其余元素全都是零。
做训练的时候，我们希望向量$s_i$尽量接近向量$y_i$，如果$s_i$接近$y_i$，说明物品塔训练的比较好，即使做随机特征变换，对物品的向量表征也影响不大。
用$y_i$和$s_i$的交叉熵作为损失函数，交叉熵就等于$-\log s_{i,i}$，把$s_{i,i}$替换成softmax函数输出的第I个数值就得到右边这一项，这就是自监督学习的损失函数，训练的时候要最小化损失函数。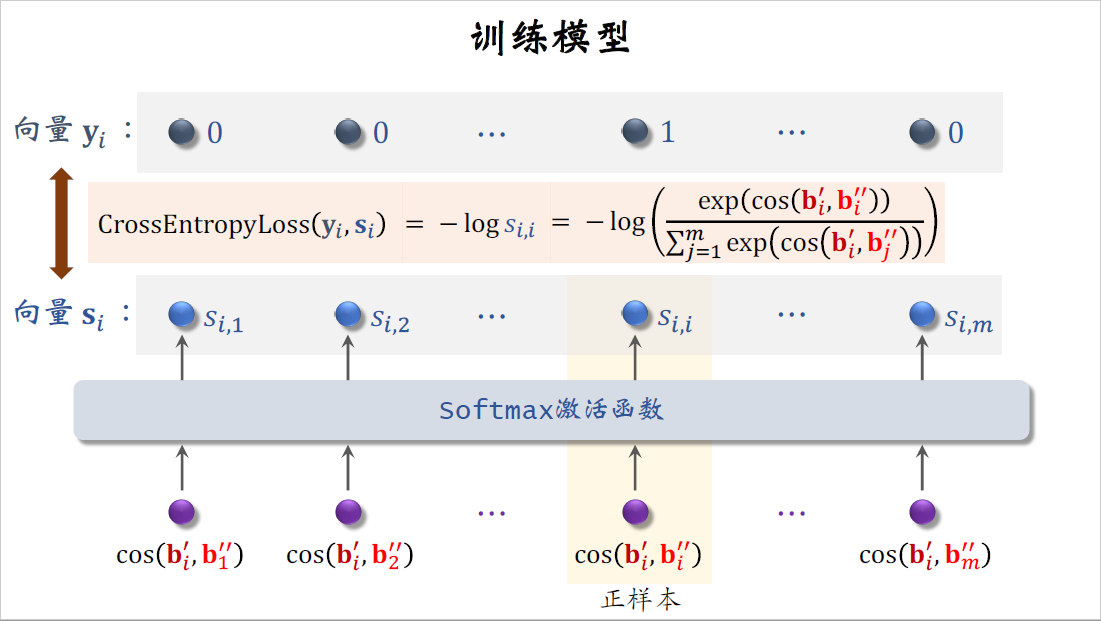

这是我们刚刚推导出的交叉熵损失函数，对应第$i$个物品，记作$L_{self}[i]$。1个batch中有$m$个物品，对$m$项损失函数取平均作为自监督学习的损失，训练的过程中要做梯度下降，让损失减小。

总结

最后总结一下这节课内容，这节课讨论了双塔模型存在的一个问题，就是双塔模型学不好低曝光物品的向量表征。
其实这不是双塔模型的问题，而是数据的问题，真实推荐系统都存在头部效应，小部分物品占据了大部分的曝光和点击，google提出一种自监督学习的方法，用在双塔模型上效果很显著，这种方法对物品做随机特征变换。对一个物品用两种特征变换，物品塔输出两个向量记作$b^{\prime}$和$b^{\prime\prime}$。对于同一个物品，用不同的特征变换，得到两个向量应该有较高的相似度，而对于不同的物品要求两个向量的相似度较低，也就是说让物品的向量表征尽量spread out，分散在整个特征空间上，而不是集中在一起。这种自监督学习方法实际效果非常好，不论是YOUTUBE自己的落地，还是我们小红书推荐的搜索，召回的复现，都取得了显著的效果，低曝光物品和新物品的推荐变得更准，这些物品的点击率，点赞率等指标都有显著的提升，整个大盘的指标也有一定的改善。

训练具体这样做，每次对点击做随机抽样，得到$n$对用户物品的二元组，作为一个batch，这个batch用来训练双塔，包括用户塔和物品塔。根据点击做抽样，热门物品被抽到的概率高，每次还要从全体物品中做均匀抽样，得到$m$个物品，作为另一个batch，这样抽样的话，热门和冷门物品被抽到的概率是相同的，这个batch用来做自监督学习，只训练物品塔，最后做梯度下降，使损失函数减小。
$L_{main}$是双塔模型的损失，一个batch有$n$个用户和$n$个物品，对他们的损失取平均，$L_{self}$是自监督学习的损失，一个batch有$m$个物品，对他们的损失取平均，中间的$\alpha$是个超参数，决定自监督学习起到的作用，这节课就讲到这里，感谢大家观看。