召回11：曝光过滤

本博文引自王树森老师推荐系统。
视频地址：召回11：曝光过滤 & Bloom Filter_哔哩哔哩_bilibili
课件地址： https://github.com/wangshusen/RecommenderSystem

这节课内容是曝光过滤和Bloom Filter，曝光过滤通常是在召回阶段做，具体的方法就是用bloom filter。

曝光过滤

曝光过滤是这样一个问题：在推荐系统中，如果用户看过某个物品，就不再把物品推荐给这个用户，小红书抖音都这样做曝光过滤，原因是实验表明，重复曝光同一个物品会损害用户体验，但也不是所有推荐系统都有曝光过滤，像youtube这样的长视频就没有曝光过滤，看过的可以再次推荐。
想要做曝光过滤，需要对于每个用户记录已经曝光给他的物品，一个用户历史上看过的物品可能会非常多，好在不需要存储所有的历史记录，只需要存储最近一段时间的就行。
以小红书推荐系统为例，只召回发布时间小于一个月的笔记，更老的笔记根本不会被召回，所以就不用对年龄大于一个月的笔记做曝光过滤，只需要记录每个用户最近一个月的曝光历史，用他们做曝光过滤。在做完召回之后，对召回的物品做曝光过滤，判断每个物品是否已经给该用户曝光过，如果已经曝光过，就需要从召回的结果中排除掉。
一位用户看过$n$个物品，本次召回了$r$个物品，如果靠暴力对比做曝光过滤，那么需要花费$2n$的时间，在小红书用户一个月的曝光量$n$的量级大约是几千，每次推荐召回量$r$的量级也是几千，暴力对比的计算量太大了，所以实践中不做暴力对比，而是用bloom filter。

Bloom Filter

bloom filter是一种数据结构，发表在1970年，以他的发明者命名。推荐系统曝光过滤基本都是用bloom filter做的，它可以判断一个物品是否在以曝光的物品集合中。如果bloom filter的判断是no，那么该物品一定不在集合中；如果bloom filter的判断是yes，我们就不是那么确定了，只能说该物品很可能在集合中，但也存在误伤的概率。Bloom Filter可能把未曝光的物品误判为已经曝光，把这个未曝光的物品给过滤掉。
概括一下，如果根据bloom filter的判断做曝光过滤，肯定能干掉所有已经曝光的物品，用户绝对不可能重复看到同一个物品，但是bloom filter有一定的概率会误伤，召回的物品明明没有曝光过，却被bloom filter给干掉了。

Bloom filter是一种数据结构，它把物品的集合表示为一个向量，这个向量是$m$维的，每个元素是一个bit，要么是零，要么是一。
每个用户都有若干曝光物品，把这些物品表征为一个向量，也就是说系统要给每个用户存一个向量，向量需要$m$bits的存储。
bloom filter有k个哈希函数，每个哈希函数把物品id映射成介于0和$m-1$之间的整数，k和$m$都是需要设置的参数，后面会讲他们设置成多大。

接下来我要讲bloom filter，如何用k个哈希函数做曝光过滤。
我先讲最简单的情况，k的取值是一，也就是说只用一个哈希函数。boom filter需要用一个二进制向量做存储，向量的长度是$m$，也就是说存储一共需要花费$m$bits。初始的时候向量是全零的。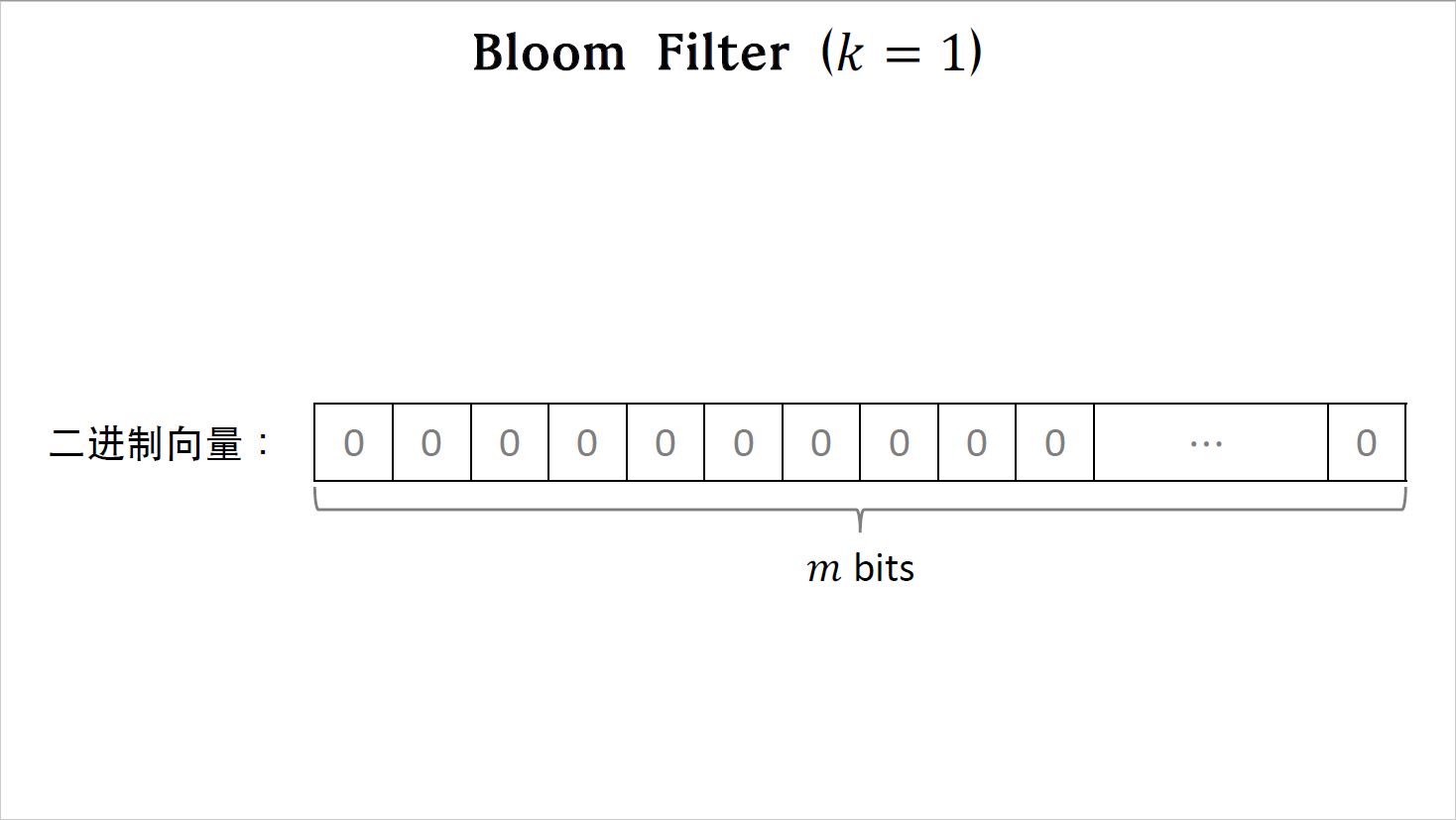

我们知道一个用户有哪些已经曝光过的物品，这是第一个物品的ID，哈希函数把它映射到这个位置，把这个位置的元素置为一；这是第二个物品的ID，哈希函数把它映射到这个位置，把这个位置的元素置为一。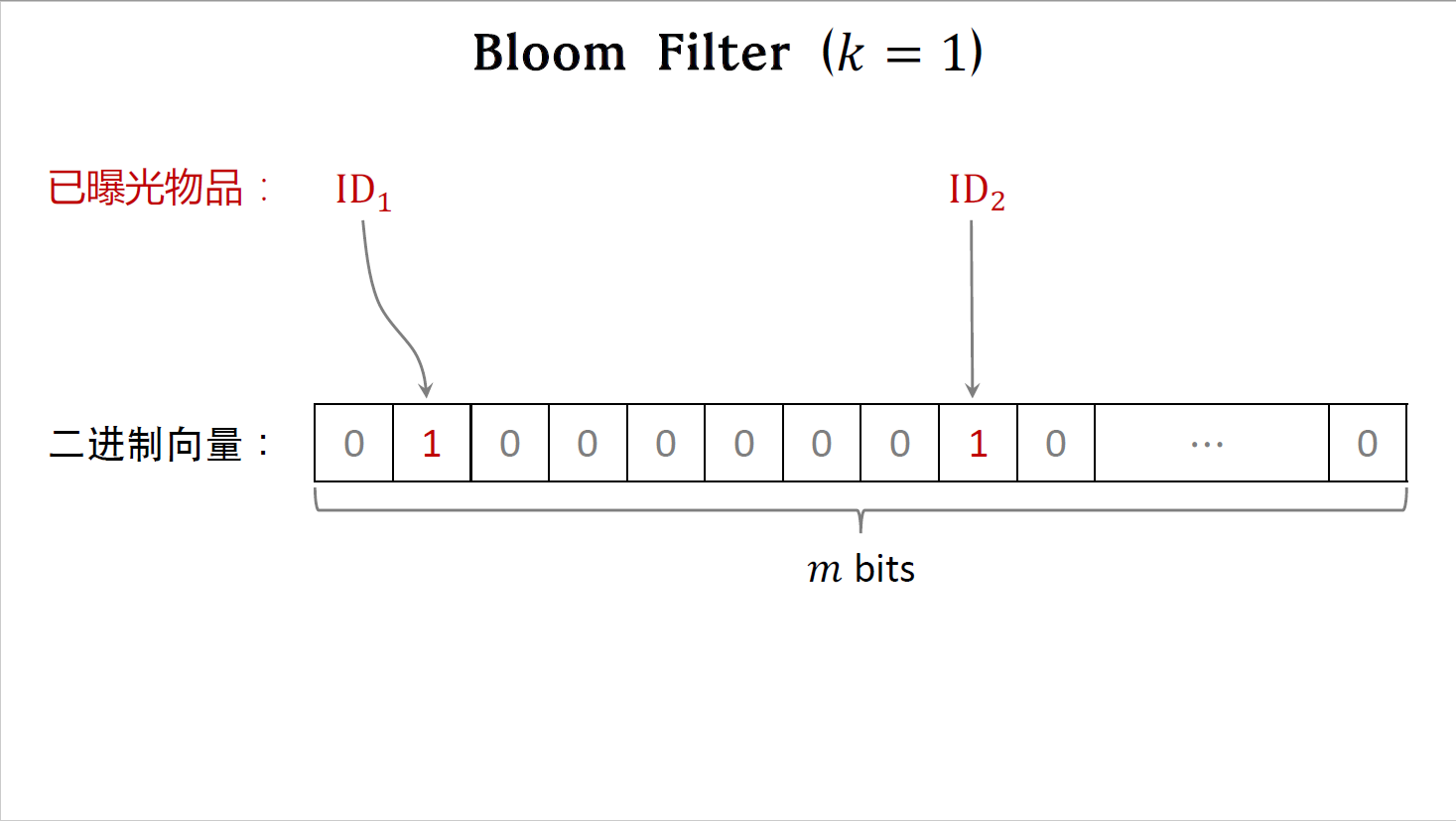

哈希函数把第三物品的ID映射到这个位置，这个位置的元素已经是一了，不需要修改这个数值；哈希函数把第四个物品的ID映射到这个位置，这个位置原本是零，现在把它置为一；哈希函数把第五第六个物品都映射到这个位置，这个位置的元素已经是一了，不需要修改这个数值。
到此为止，我们已经把六个物品表征为一个向量，这个向量的元素有零，有一。

我们来看一下如何利用这个向量做曝光过滤，用户发起推荐请求之后召回很多物品，这是其中一个，它($ID_7$)之前没有曝光给用户，它被映射到这个位置，这里的元素是零，所以bloom filter判断这个物品之前没有曝光，这个判断是正确的，如果bloom filter认为没有曝光，那么这个物品肯定没有曝光。bloom filter不可能把已曝光的物品错判为未曝光。
这个物品($ID_5$)已经曝光，哈希函数把它映射到这个位置，这里的元素是一，意思是bloom filter认为这个物品已经曝光，bloom filter的判断是正确的。

这个物品($ID_8$)没有曝光，哈希函数把它映射到这个位置，这里的元素是一，bloom filter认为这个物品已经曝光，但这其实是个误判，bloom filter有一定概率，把未曝光的物品误判为已曝光，导致未曝光的物品被过滤掉，造成误伤。

刚才讲解了简化版的bloom filter，哈希函数的数量是k=1。接下来的例子中，哈希函数的数量是k=3。
初始的时候，二进制向量的元素全都是零。

这是个已经曝光的物品($ID_1$)，需要记录到向量上。k=3，所以用三个不同的哈希函数，把物品ID映射到三个位置上，把这三个位置上的元素全都置为一。
这也是个以曝光的物品($ID_2$)，用三个哈希函数把物品ID映射到三个位置上，把这三个位上的元素都置为一，如果某个位置的元素本身就是一，那么它不用被修改。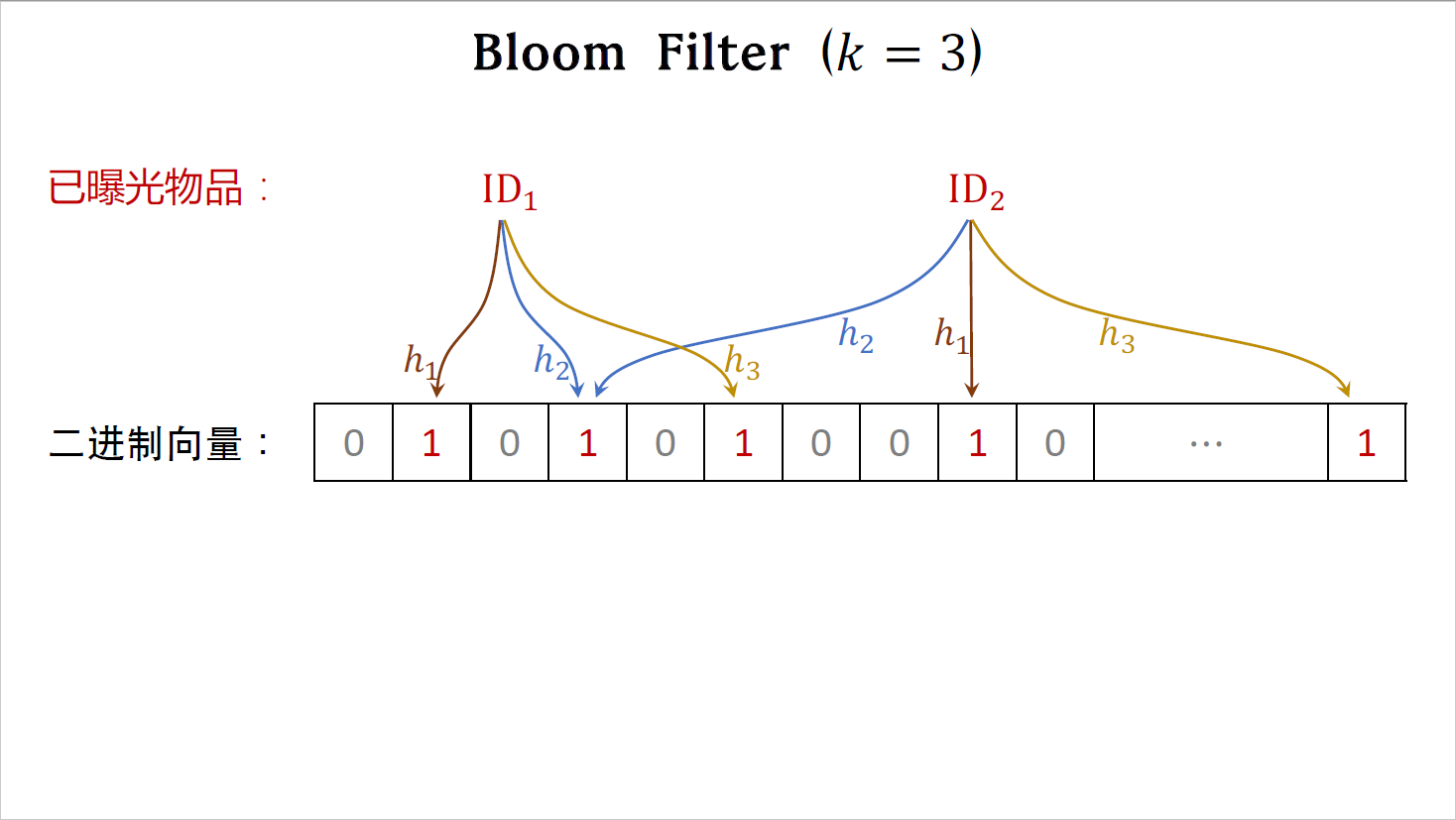

这是个召回的物品($ID_8$)，没有曝光，三个哈希函数把物品ID映射到这三个位置，假如这个物品已经曝光，那么三个位置上肯定都是一，但其中一个位置是零，说明这个物品未曝光，如果bloom filter判断物品未曝光，那么他一定没有曝光，bloom filter不会犯错。
这个召回的物品($ID_4$)已经曝光过，三个哈希函数把物品ID映射到这三个位置上，由于三个位置全都是一，bloom filter判定它已经曝光，会把这个物品给过滤掉，这个判断是正确的。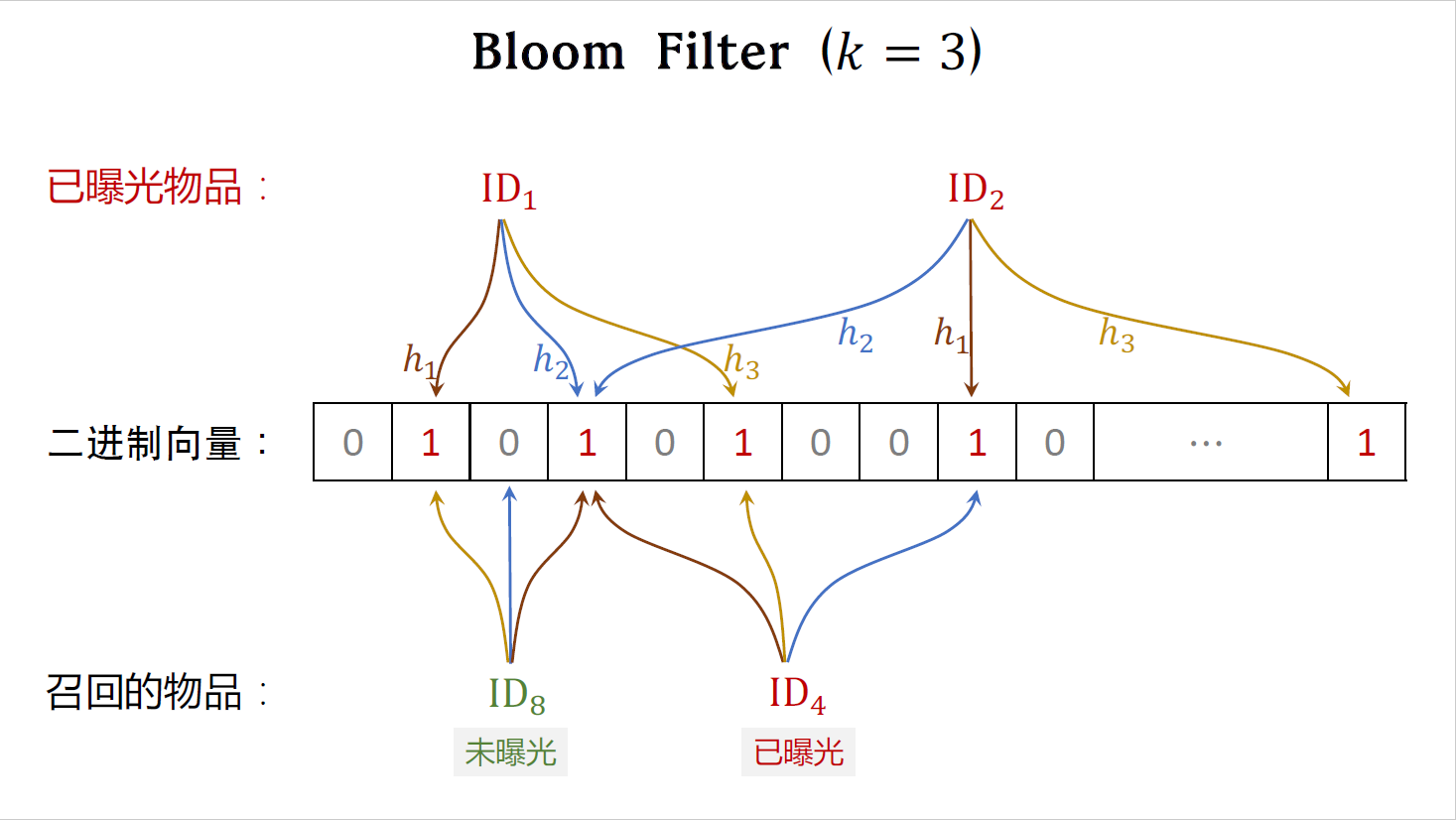

这个召回的物品还没有曝光，三个哈希函数把物品ID映射到这三个位置，由于三个位置全都是一，bloom filter判断这个物品已经曝光过，这其实是个误判。前面说过，bloom filter有一定概率，把未曝光的物品判定为已曝光，导致未曝光的物品被过滤掉，造成误伤。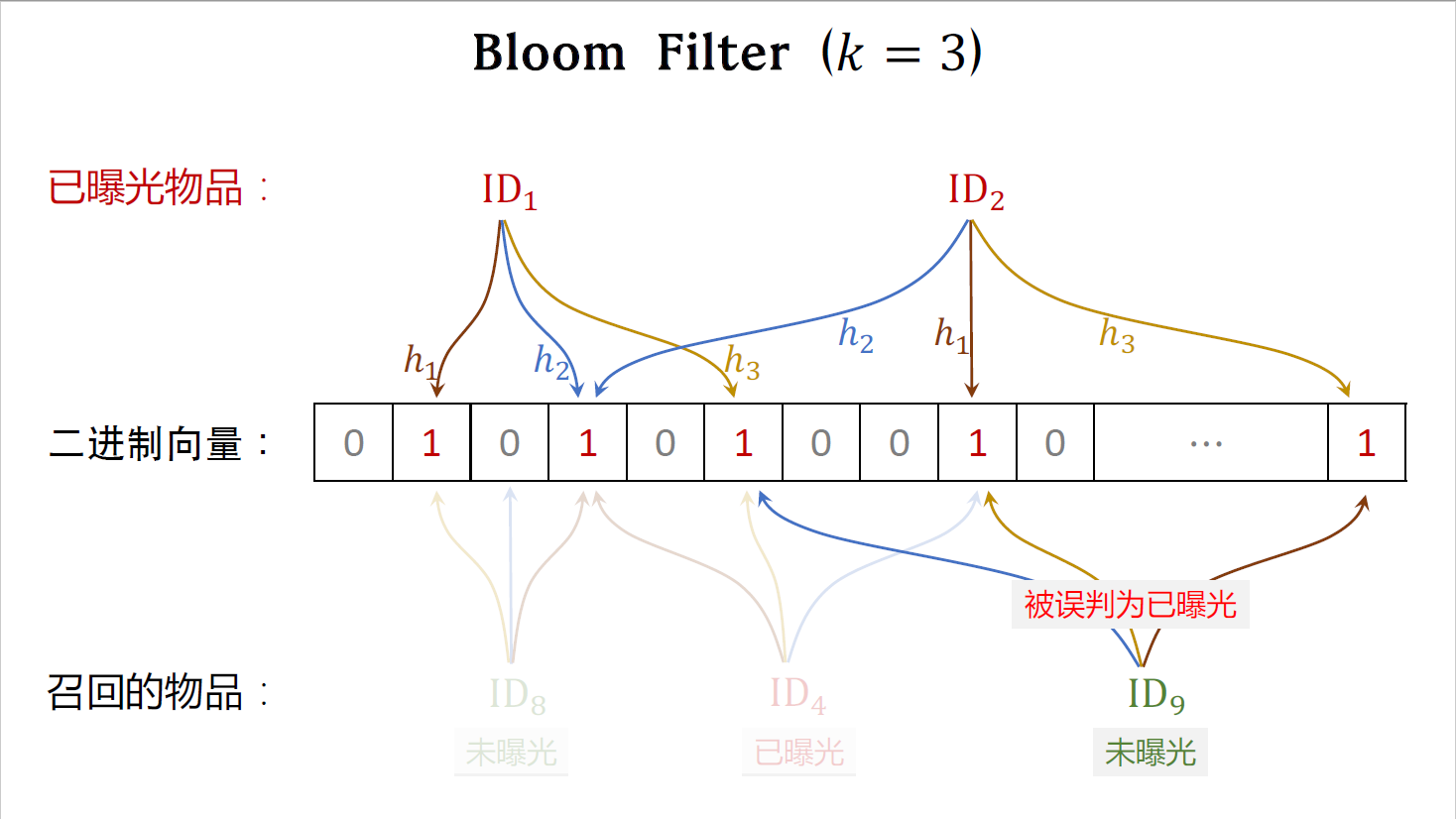

我们来分析一下bloom filter误伤的概率，定义$n,m,k$这三个数，曝光物品的集合大小为$n$，二进制向量的维度为$m$，使用$k$个哈希函数。
这个公式给出了误伤概率$\delta$的大小，$\delta$取决于$n,m,k$这三个数。
$n$越大，也就是曝光物品数量越多，那么误伤的概率就会越大。这是很显然的，曝光物品越多，往二进制向量写的一就越多，那么bloom filter就越容易出现误伤，如果向量中的一很多，那么未曝光的物品的$k$个位置，很可能恰好全都是一被误判为已经曝光。
$m$是二进制向量的长度，$m$越大，两个物品的哈希值就越不容易冲突，出现误伤的概率就越小，但是$m$越大需要的存储就越多。
$k$是哈希函数的数量，太大或者太小都不好，它的大小有最优值。

人为设定可容忍的误伤概率为$\delta$，比方说能容忍1%的错误，那么设置$\delta$等于1%。
确定了误伤概率$\delta$，那么就有最优的参数$k$和$m$，哈希函数数量$k$是个很小的整数，$k=1.44\ln{\frac{1}{\delta}}$，设置$m=2n\ln{\frac{1}{\delta}}$。$m$的大小正比于$n$，$m$比$n$大几倍。也就是说，每个曝光物品只需要占几个bit的存储，用户历史记录上有$n$个曝光物品，只需要$m$等于$10n$ bits，就可以把误伤概率降低到1%以下。

曝光过滤的链路

接下来我要讲推荐系统中曝光过滤的链路。这是推荐系统的链路(上半)，用多路召回，然后经过粗排精排重排，最终选出一批物品曝光给用户。
这是曝光过滤的链路(下半)，把曝光的物品记录下来，更新bloom filter用于过滤召回的物品。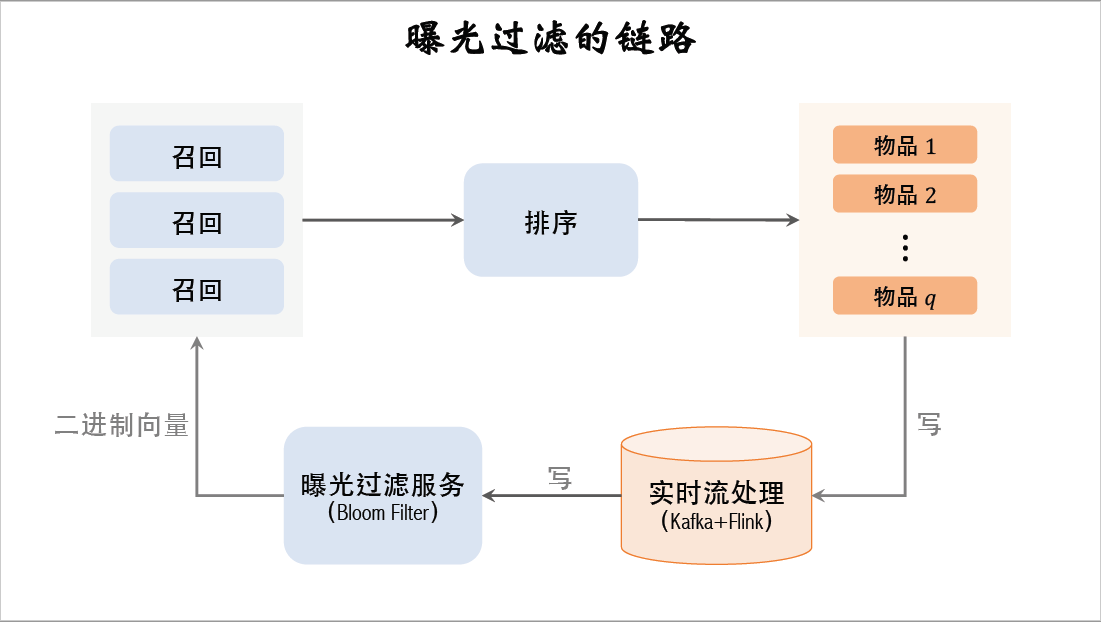

App的前端有埋点，所有曝光的物品都会被记录下来，这个落表的速度要足够快，否则可能会出问题。用户推荐页面两次刷新也就间隔几分钟，快的话也就是一二十秒，在下一刷之前，就要把本次曝光的结果写到bloom filter上，否则下一刷很可能会出重复的物品。所以要用实时流处理，比如把曝光物品写入Kafka消息队列，用flink做实时计算。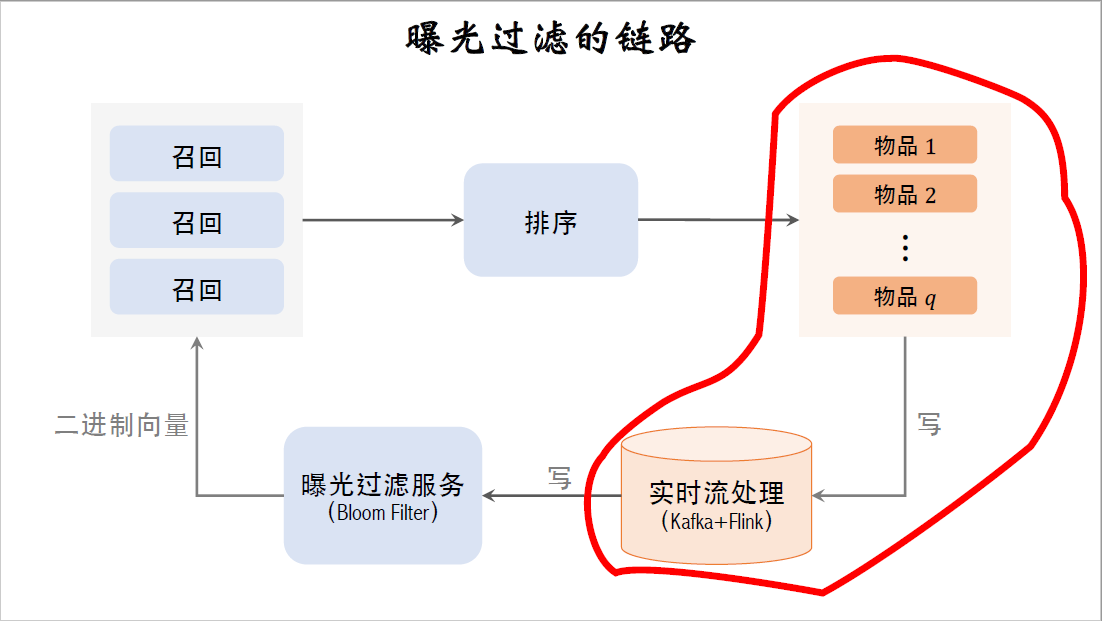

flink实时读取Kafka消息队列，计算曝光物品的哈希值，把结果写到bloom filter的二进制向量上。用这样的实时数据链路，在曝光发生几秒之后，这位用户的bloom filter就会被修改之后，就能避免重复曝光。
但实时流这部分也是最容易出问题的，如果挂掉了或者延迟特别大，那么用户上一刷在看过的物品又会出现。小红书的首页推荐以前经常出这种问题。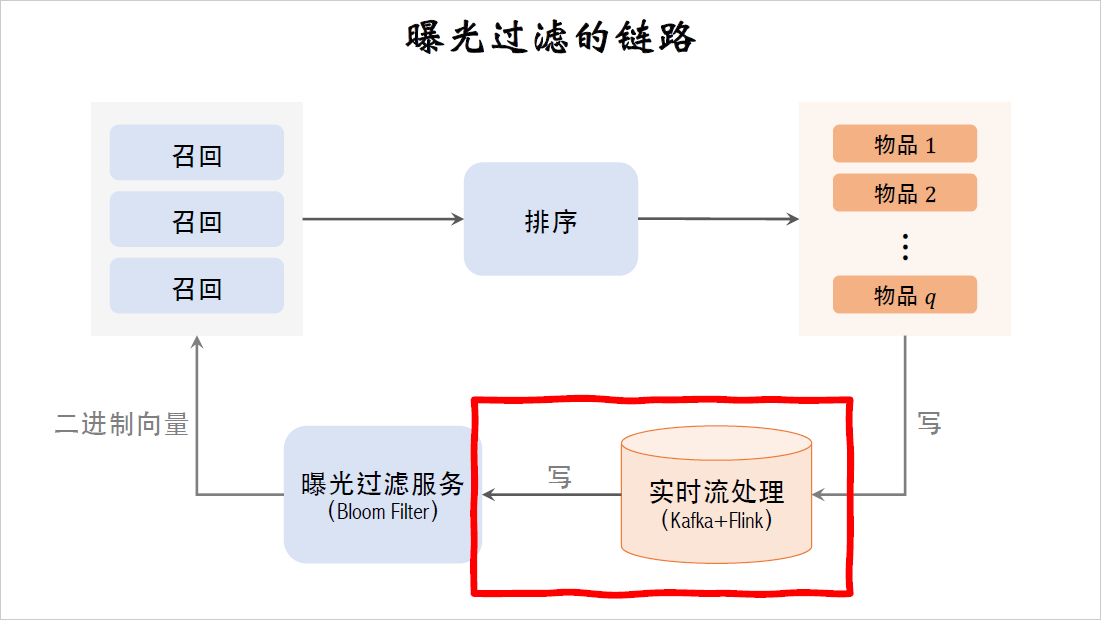

曝光过滤具体用在召回完成之后。召回服务器请求曝光过滤服务，曝光过滤服务把这位用户的二进制向量发送给召回服务器，在召回服务器上，用bloom filter计算召回的物品的哈希值，再跟二进制向量做对比，把已经曝光的物品给过滤掉，剩余的物品都是未曝光的，发送给排序服务器。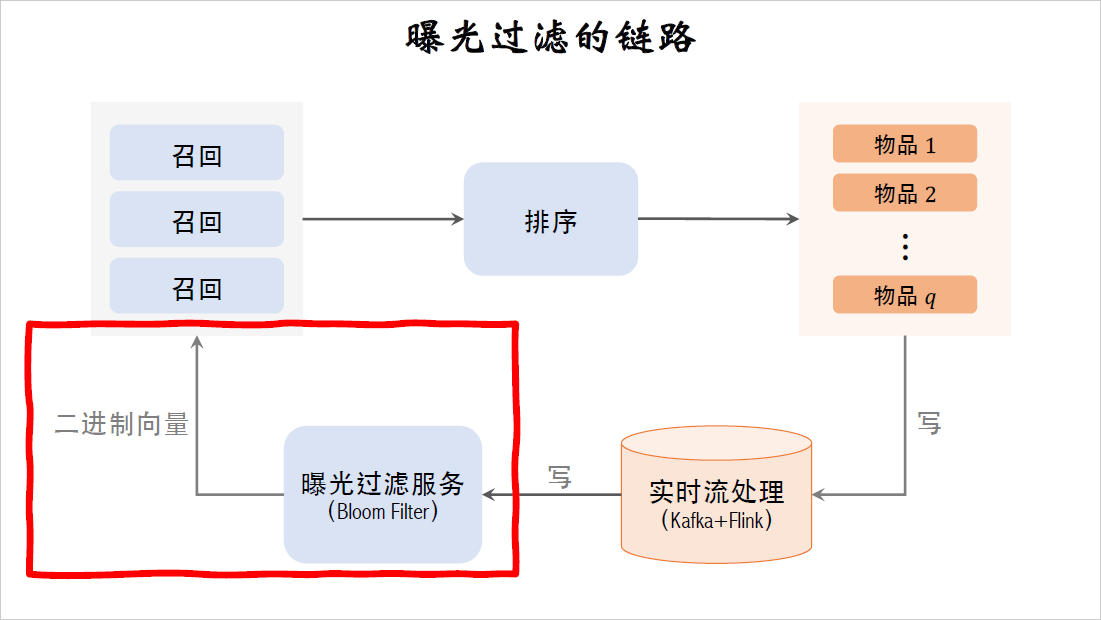

Bloom Fliter的缺点

我已经讲完了，推荐系统如何在召回阶段做曝光过滤。最后说一下boon filter这种数据结构的缺点：bloom filter把物品的集合表示成一个二进制向量，每往集合中添加一个物品，只需要计算出k个哈希值，然后把向量k个位置的元素值为一，k是哈希函数的数量。如果向量的元素本来就是一，那么就不需要做修改。
bloom filter有个缺点，只能添加物品，不支持删除物品，如果从集合中移除掉一个物品，没有办法消除这个物品对二进制向量的影响，不能简单把这个物品对应的k个元素，从一改成零，否则会影响其他物品，这是因为向量的元素是所有物品共享的，如果把向量的一个元素改成零，相当于把很多物品都移除掉了。
实践中，每天都需要从物品的集合中移除掉年龄大于一个月的物品。原因是这样的，小红书的首页只推荐年龄小于一个月的物品，超出一个月的物品不可能被召回，那么就没有必要对他们做曝光过滤，没有必要把它们记录在bloom filter的向量上。移除掉超龄物品，那么曝光物品的数量$n$会减小，误伤率会降低，对业务有好处，但可惜的是，bloom filter不支持物品的删除，想要删除一个物品，需要重新计算整个集合的二进制向量。

这节课讲了推荐系统中的曝光过滤问题，以及bloom filter这种数据结构，这节课就讲到这里，感谢大家观看,