排序02：Mixture-of-Experts（MMoE）

本博文引自王树森老师推荐系统。
视频地址：排序02：Multi-gate Mixture-of-Experts (MMoE)_哔哩哔哩_bilibili
课件地址： https://github.com/wangshusen/RecommenderSystem

上节课介绍最简单的多目标排序模型，这节课介绍一种改进的模型，叫做multgate mixture of experts，缩写是MMoE。
跟上节课一样，模型的输入是一个向量，包含用户特征，物品特征，统计特征，还有场景特征。
把向量输入三个神经网络，这三个神经网络结构相同，都是由很多全连接层组成，但这三个神经网络不共享参数。三个神经网络各输出一个向量，三个向量叫做$x_1$，$x_2$，$x_3$ ，这三个神经网络被叫做专家，就是mixture of experts中的experts，这里我是为了画图方便，用了三个专家神经网络，实践中通常会试一试四个或者八个。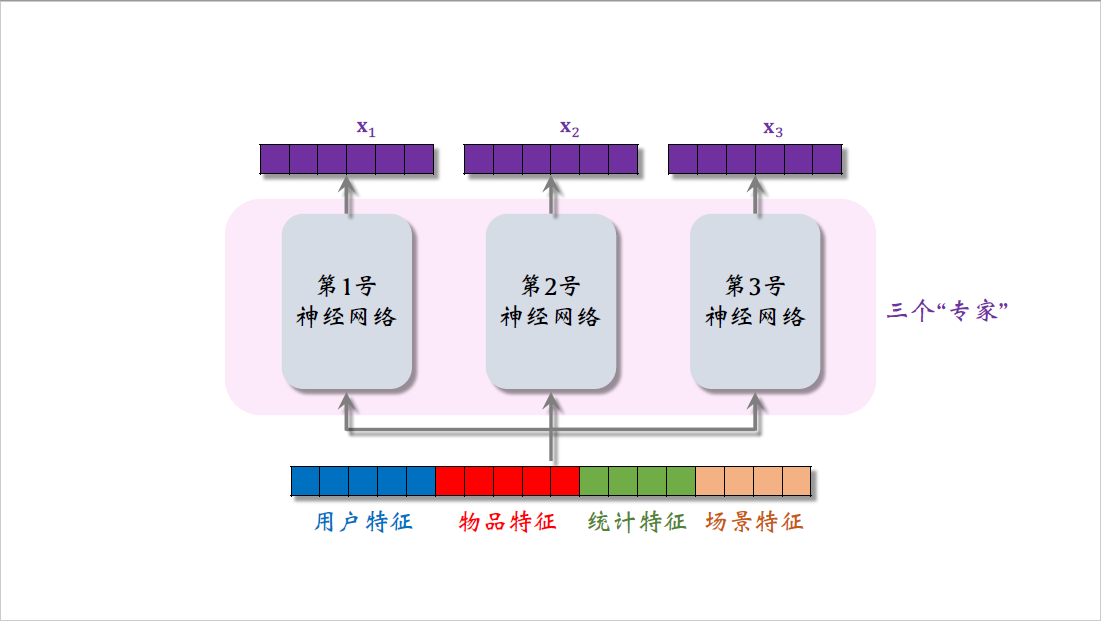

把下面的特征向量输入另一个神经网络，这个神经网络也有多个全连接层，在神经网络的最后加一个softmax激活函数，输出一个三维的向量，由于是softmax输出，向量的三个元素都大于零，而且相加等于一。
向量的三个元素记作$p_1$，$p_2$，$p_3$ ，分别对应三个专家神经网络之后，我们会用这三个元素作为权重，对向量$x_1$，$x_2$，$x_3$ 做加权平均.同样的方法，把下面的特征向量送入右边的神经网络，在神经网络的最后也是softmax激活函数输出一个三维向量，元素分别记作$q_1$，$q_2$，$q_3$ ，这三个元素也是之后做加权平均值的权重。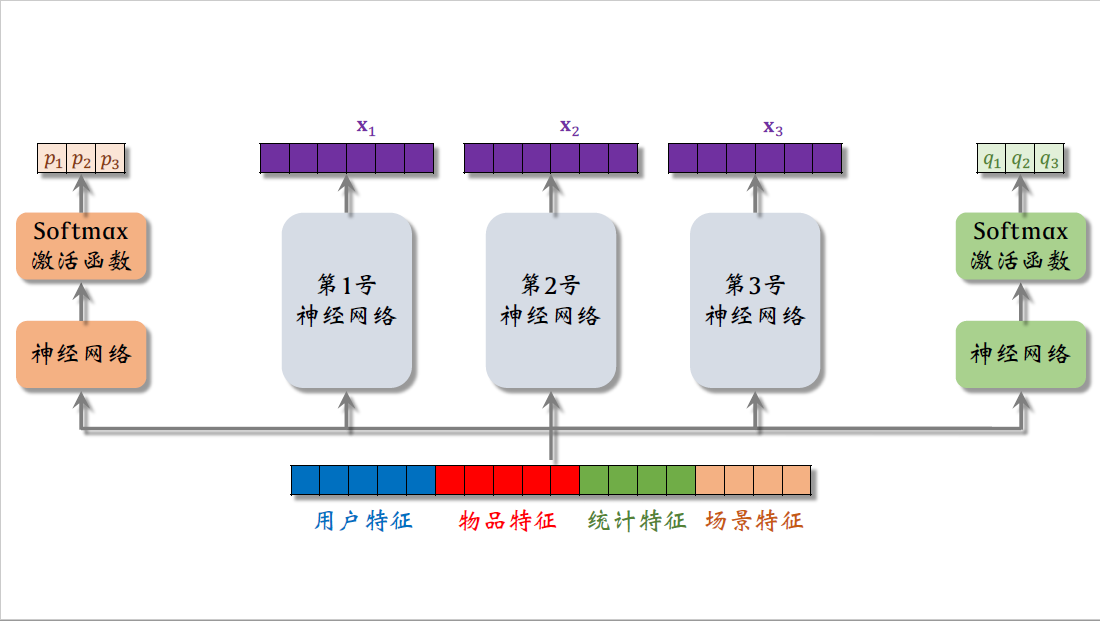

接下来我研究更上层的结构，刚才我说了$p_1$，$p_2$，$p_3$ 和$q_1$，$q_2$，$q_3$ 都是权重，用于之后的加权平均。
对向量$x_1$，$x_2$，$x_3$ 做加权平均，权重是$p_1$，$p_2$，$p_3$ ，得到上面的向量，它等于$p_1x_1 + p_2x_2 +p_3x_3$，就是三个紫色向量的加权平均。
用右边的权重$q_1$，$q_2$，$q_3$ 对向量$x_1$，$x_2$，$x_3$ 做加权平均，得到右边的向量，它等于$q_1x_1 + q_2x_2 +q_3x_3$，它也是三个紫色向量的加权平均，区别在于权重不同。
把左边的向量输入一个神经网络，神经网络可以有一个或者多个全连接层，神经网络的输出取决于具体的任务，比如神经网络输出对点击率的预估是一个介于0~1之间的实数。
把右边的向量输入另一个神经网络，这个神经网络会输出另一个指标的预估，比如对点赞率的预估也是介于0~1之间的实数。
我这里假设多目标模型只有点击率和点赞率这两个目标，所以用了$p$和$q$这两组权重，假如有十个目标，那么就要用十组权重。
到此为止，我已经讲完了MMoE模型的结构，模型很简单，就是对神经网络输出的向量$x_1$，$x_2$，$x_3$ 做加权平均，然后用加权平均得到的向量去预估某个业务指标。

在这个例子中需要预估点击率和点赞率这两个指标，我用了三个专家神经网络，专家神经网络的数量是个超参数，需要手动调，通常来说会试一试四个和八个。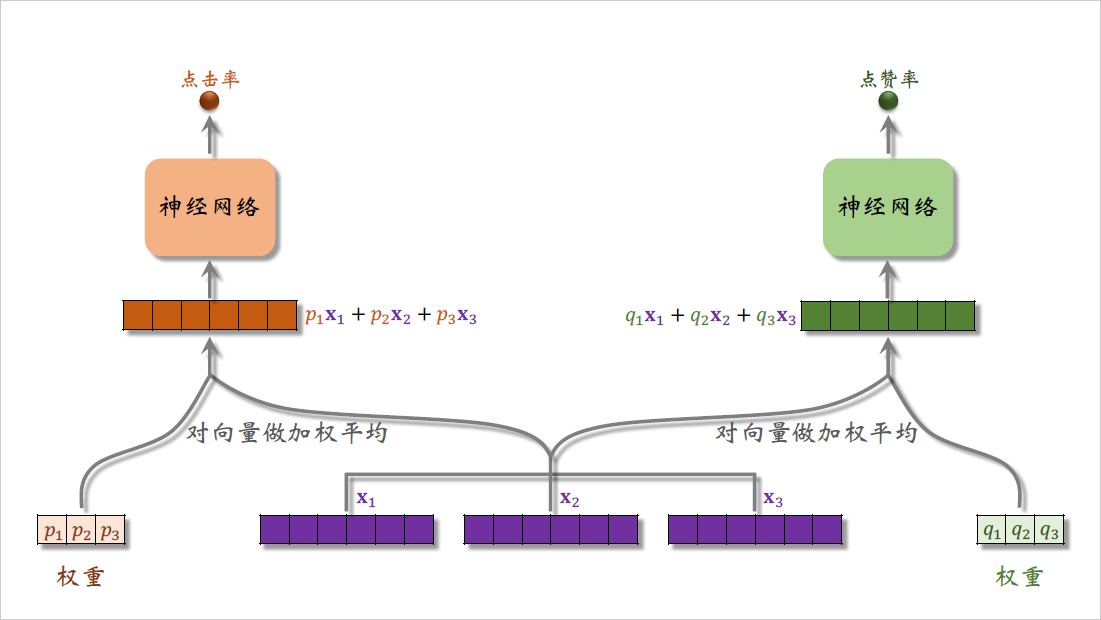

极化现象

在实践中大家都发现MMoE有个问题，就是softmax会发生极化，下面我要讲极化现象以及解决方案。
我们的例子中有两个softmax函数，各自输出一个三维向量，每个向量都是概率分布，元素大于零，相加等于一。
极化的意思是softmax输出的向量中一个值接近一，其余值接近零。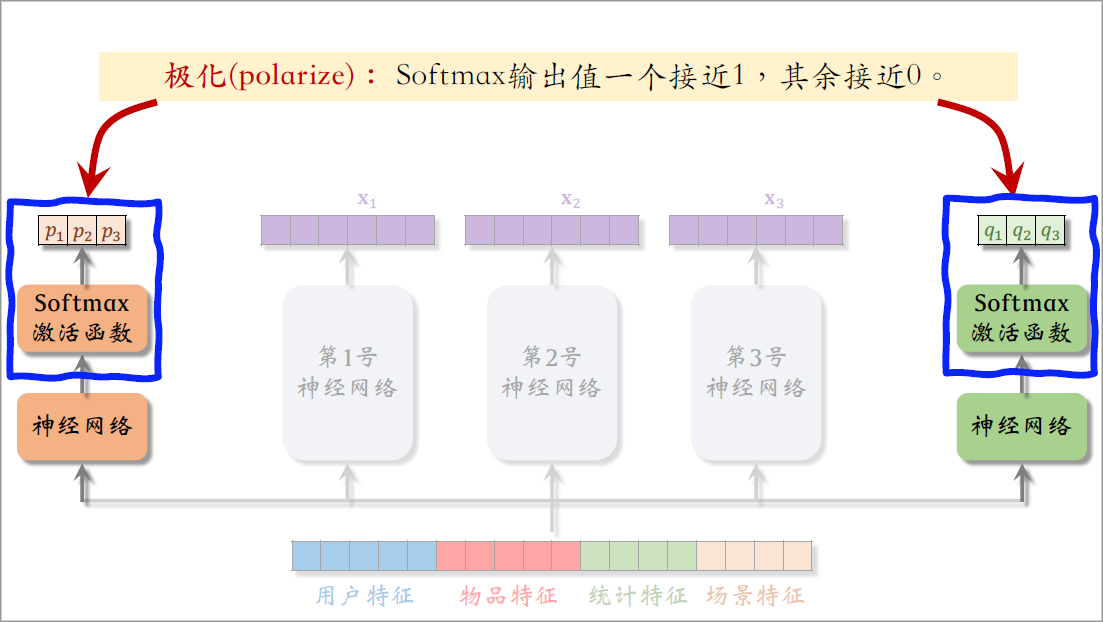

举个例子，比如左边的softmax输出值约等于0、0、1，也就是说左边的预估点击率任务只使用了第3号专家神经网络，而没有使用其他两个专家神经网络，这样就等于没有用mixture of experts，没有让三个专家神经网络的输出融合，而是简单使用了一个专家。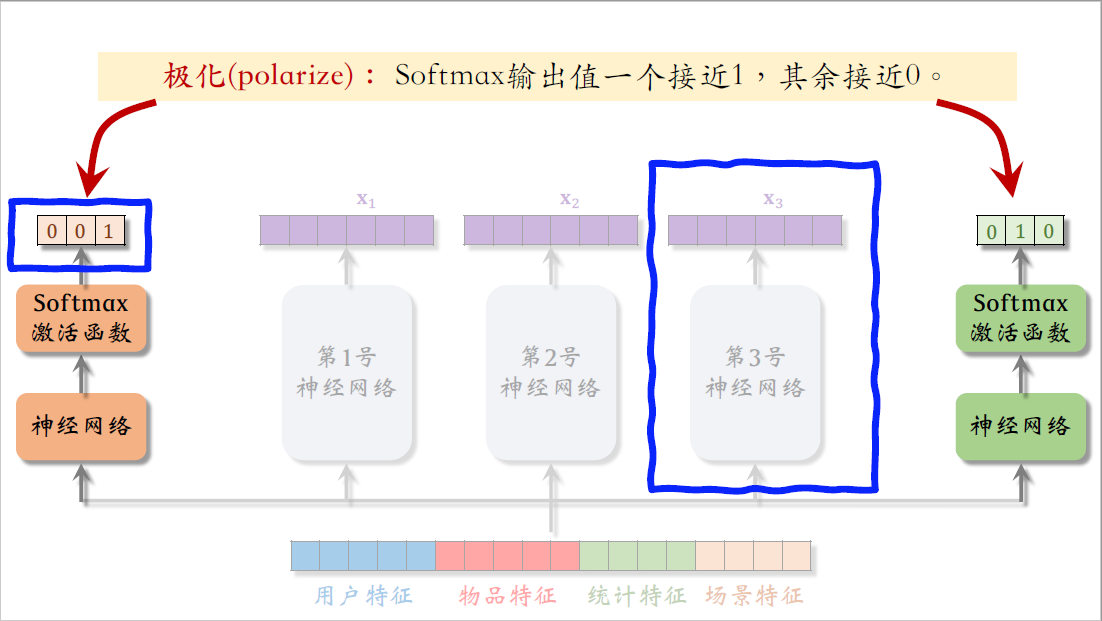

再看右边softmax的输出值接近0、1、0，也就是说右边的任务只使用了第2号专家神经网络，也没有对三个专家做融合。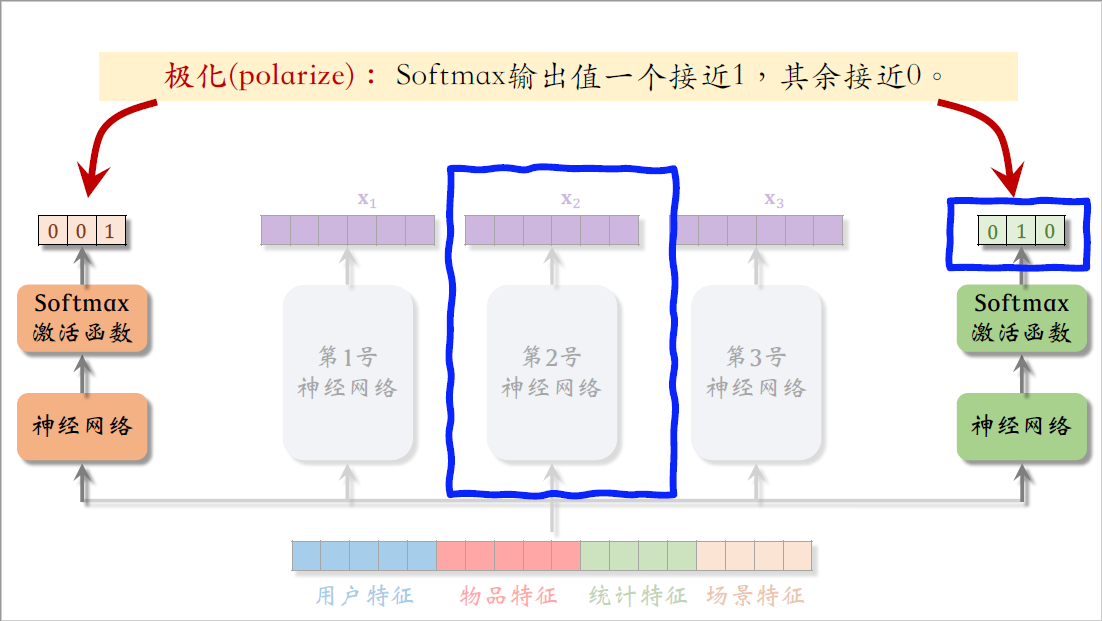

两个任务分别使用了第2号和第3号专家神经网络，这样的话第1号专家神经网络就相当于死掉了，不会被用到，那么MMoE就相当于一个简单的多目标模型，不会对专家做融合，失去了MMoE的优势，我们不希望这种现象出现。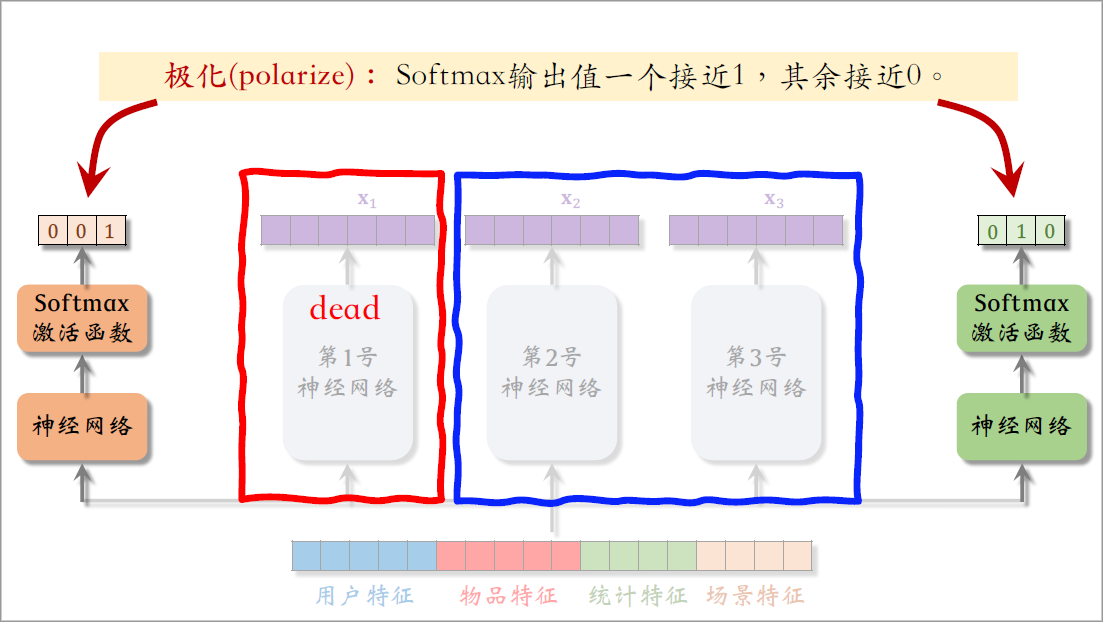

当然是有办法解决极化现象的，如果有$n$个专家神经网络，那么每个softmax激活函数的输入和输出都是$n$维向量，我们不希望看到其中一个输出的元素接近一，其余$n-1$个元素接近零。
解决极化现象的一种方法是dropout，在训练的过程中，对softmax输出使用dropout，softmax输出的$n$个数值被$mask$的概率都是10%，也就是说在训练的过程中，每个专家被丢弃的概率都是10%，这样会强迫每个任务根据部分专家做预测，如果用dropout不太可能会发生极化，否则预测的结果会特别差，假如发生极化，softmax输出的某个元素接近1，万一这个元素被$mask$，预测的结果肯定会错的离谱，为了让预测尽量精准，神经网络会尽量避免极化的发生，避免softmax输出的某个元素接近一，用了dropout，基本上能避免发生极化。

下面列了两篇参考文献，第一篇是google的，他们提出了MMoE模型，第二篇论文是youtube的，他们提出了对极化问题的解决方案。

最后提一句，不要以为把MMoE用上就一定会有提升，我跟很多算法工程师聊过，有人用MMoE之后有提升，有人用了之后就没有。MMoE没效果的原因不清楚，可能是实现不够好，也有可能是不适用于特定的业务场景，如果你们公司没有用MMoE，很可能是尝试之后发现没有提升，这节课内容讲完了，感谢大家观看。