排序04:视频播放建模
本博文引自王树森老师推荐系统。
视频地址:排序04:视频播放建模_哔哩哔哩_bilibili
课件地址: https://github.com/wangshusen/RecommenderSystem
上节课介绍了预估分数的融合,这节课专门讨论视频播放的建模,讨论播放时长和完播率这两个指标。
视频的播放时长
先来研究视频的播放时长。
图文笔记排序和视频的排序有显著的区别,对于图文笔记排序的主要依据是这些指标,包括点击、点赞、收藏、转发、评论,也就是说用户的点击和交互反映出用户对图文笔记的兴趣。
视频有些区别,视频的排序依据还有播放时长和完播,尤其是对于一些视频网站,时长和完播是最主要的指标,其次才是点击和交互。如果用户把一个视频看完,即便没有点赞、收藏、转发,也能说明用户对视频感兴趣。
我们先来讨论播放时长,由于它是个连续变量,大家自然而然会想到用回归拟合播放时长,但直接做回归的效果并不好。实践中对播放时长建模最好的方法是下面这篇youtube的论文,接下来我要讲这篇论文的方法,但我讲的跟这篇论文有些区别,原因是直接用这篇论文的方法会有偏差。
这是排序模型用的特征,其中包含用户特征、视频特征、场景特征、统计特征。把它输入多层神经网络,这个神经网络叫做shared bottom,被所有任务共享。在这个神经网络之上有很多个全连接层,每个全连接层对应一个目标,比如点击、点赞、收藏、播放时长。
这节课我们忽略掉点击点赞收藏之类的预估目标,我们只关心对播放时长的预估。最右边的输出对应播放时长,把全连接层输出的实数记作$z$,后面要用到它。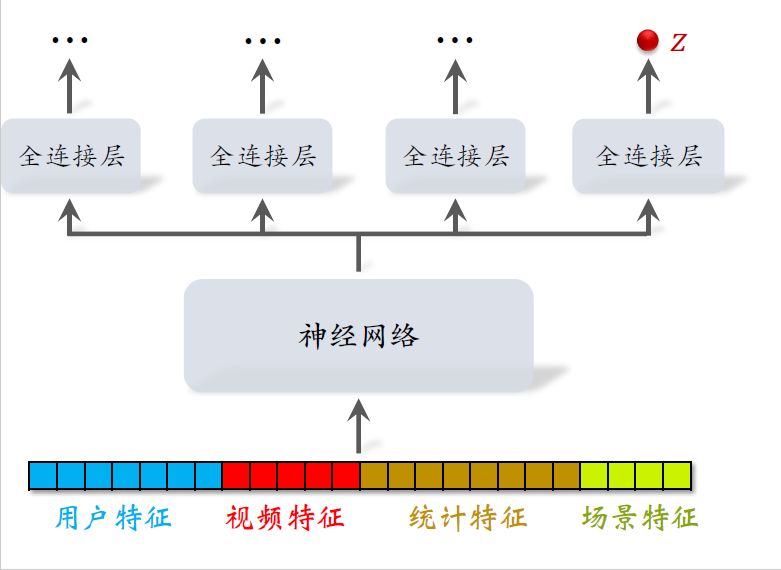
对$z$做sigmoid变换,得到$p$。
根据sigmoid函数的定义,我们让$p$拟合$y$,$y$是我们自己定义的,$$y=\frac{t}{1+t}
$$$t$的意思是用户实际观看视频的时长,$t$越大,则$y$也越大。
为了让$p$拟合$y$,我们用$y$和$p$的交叉熵作为损失函数,它等于$y·\log p + (1-y) · \log {(1-p)}$,最小化交叉熵会让$p$接近$y$。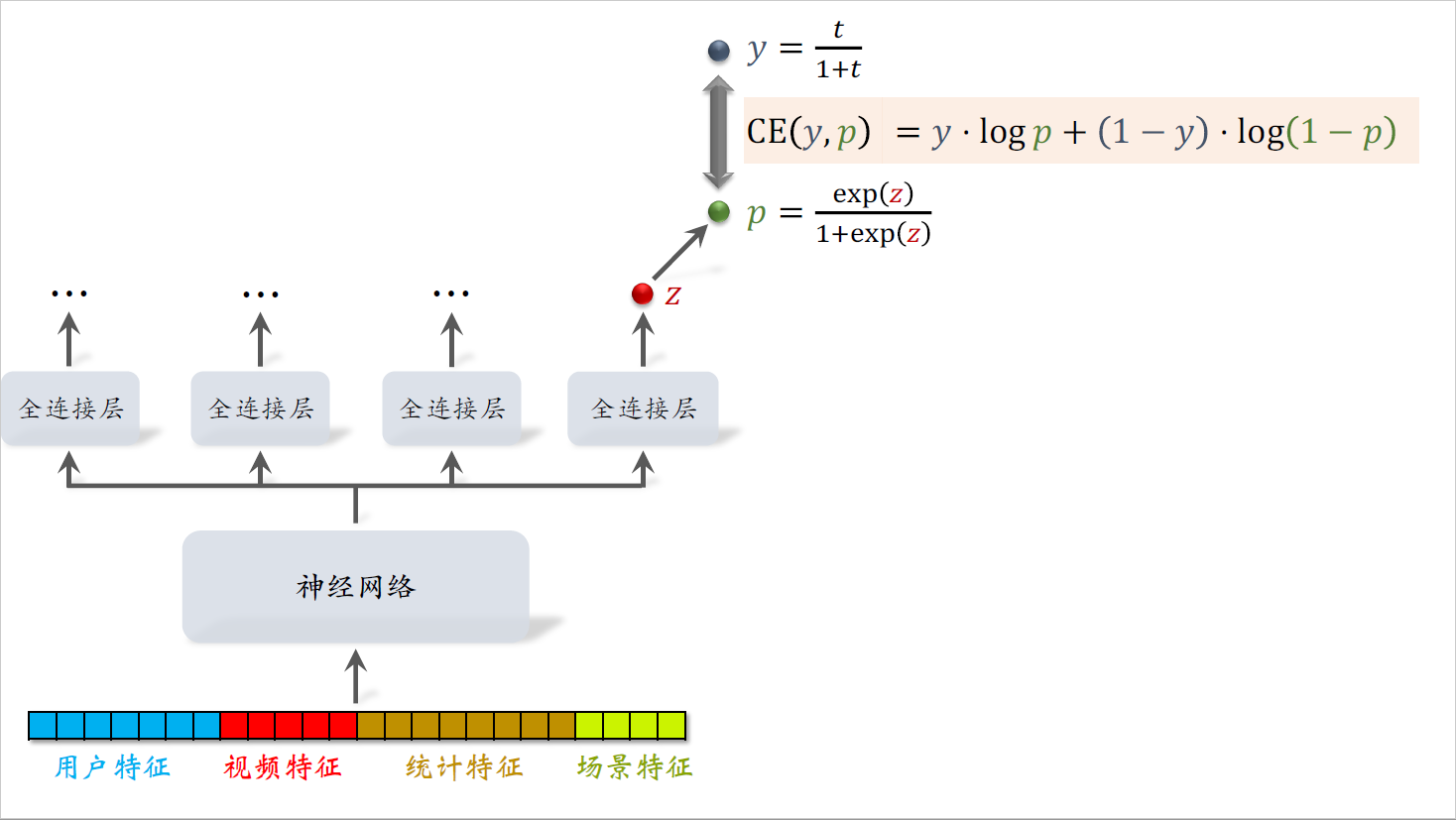
大家仔细看一下$p$和$y$。$p$等于$\frac{\exp(z)}{1+\exp(z)}$,而$y$等于$\frac{t}{1+t}$,很显然,如果$p$等于$y$,那么$\exp (z)$就等于$t$,也就是说我们可以用$\exp (z)$作为播放时长的预估。$z$在这里,对$z$做指数变换输出的实数$\exp (z)$就是对播放时长的预估。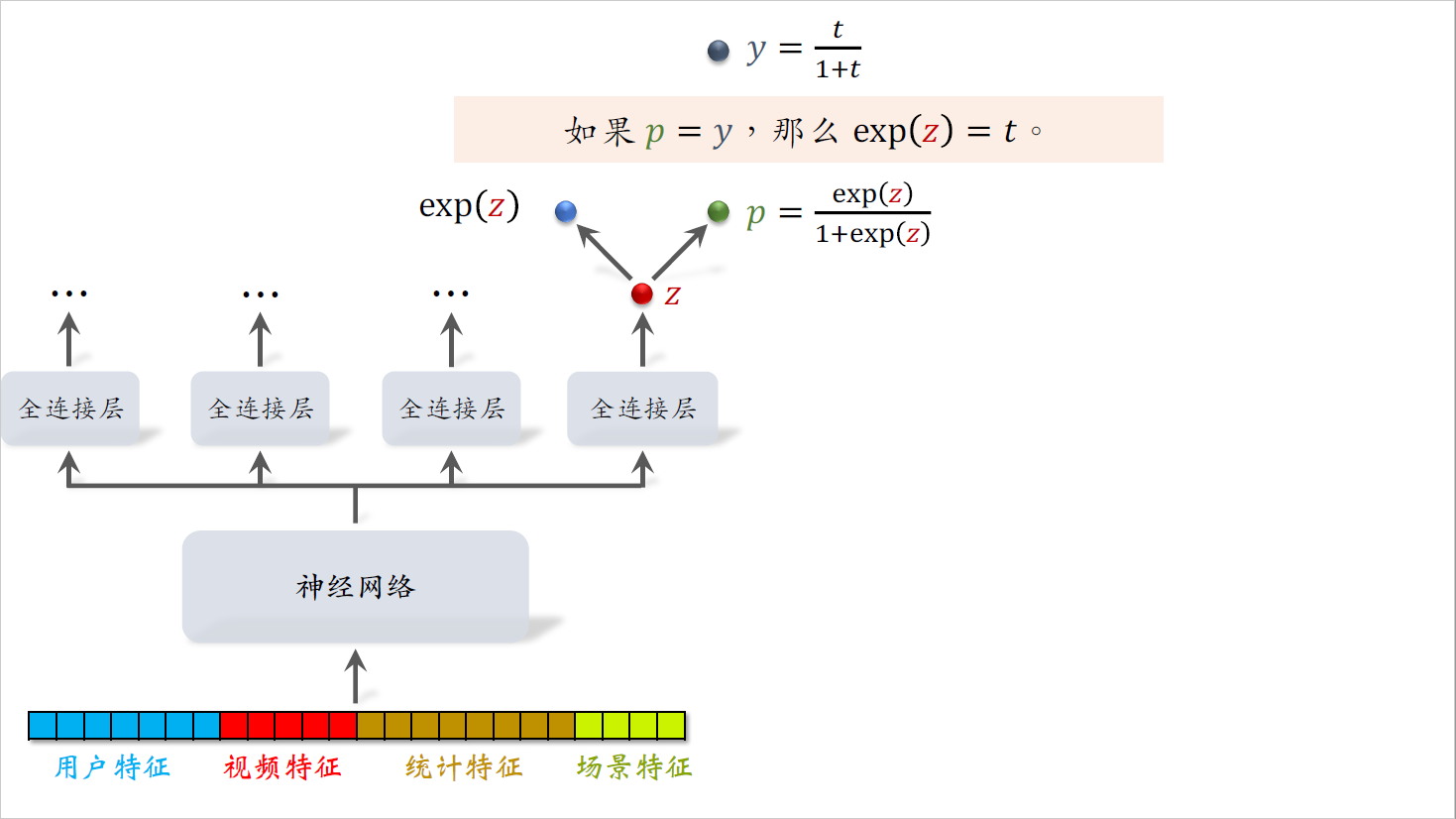
总结一下,右边的全连接层输出$z$,对$z$做sigmoid变换得到$p$。在训练中要用$p$,用$y$与$p$的交叉熵作为损失函数训练模型,做完训练之后,$p$就没有用了。线上做推理的时候,只用$z$的指数函数,把它作为对播放时长$t$的预估。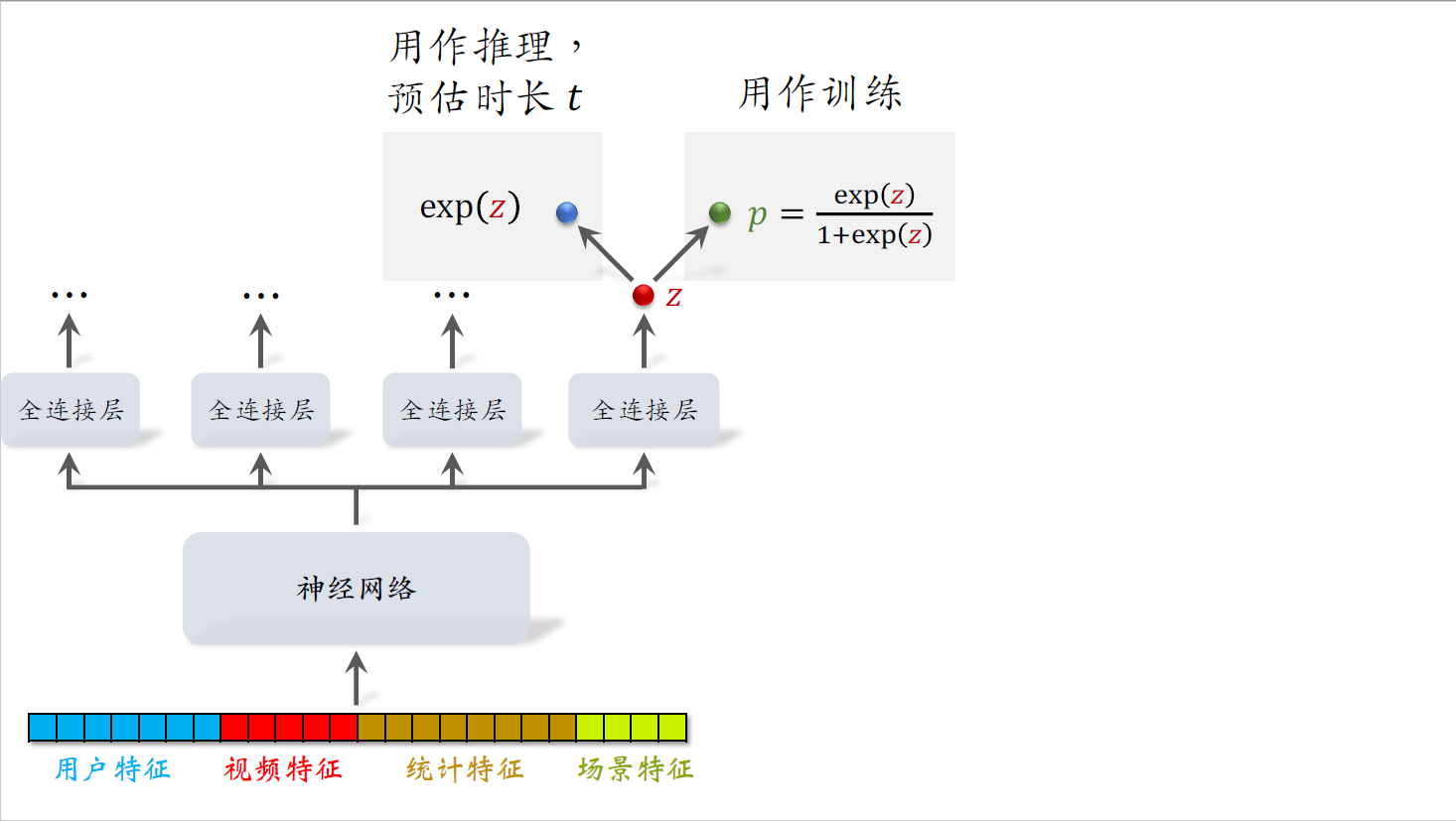
再重复一遍视频的播放时长建模,具体这样做:
把最后一个全连接层的输出记作$z$,$z$是个实数,可以是正的,也可以是负的。在训练的时候要用到$p$,它等于$z$的sigmoid函数。
我们把实际观测到的播放时长记作$t$。$t$被记录在训练数据中,如果用户没有点击视频,那么$t$就等于零。
做训练的时候到最小化交叉熵损失函数,前面我解释过这个交叉熵损失函数是怎么来的。
实践中把分母$(1+t)$给去掉也没问题,这就相当于给损失函数做加权,权重是播放时长。
线上做推理的时候,把$\exp (z)$作为对播放时长的预估。
最终把$\exp(z)$作为融分公式中的一项,它会影响到视频的排序。
视频完播
前面介绍我对播放时长的预估,这节课剩下内容是对视频完播的预估。
对于视频完播有两种建模的方法,一种是回归。
举个例子,视频的长度是十分钟,用户实际播放了四分钟就关掉了,那么实际的播放率是$y=0.4$。
做训练的时候,让模型预估的播放率$p$去拟合$y$。$y$的大小介于0~1之间,用$y$和$p$的交叉熵作为损失函数。
在线上用$p$作为对完播率的预估,比方说模型输出$p=0.73$,意思是预计播放73%。
这个预估的完播率就像是点赞率,收藏率一样,反映出用户对物品的兴趣,预估的完播率会作为融分公式中的一项影响视频的排序。
另一种视频完播的建模方法,是二元分类。
需要算法工程师自己定义完播指标,比如完播80%。什么意思呢,如果一个视频的长度是十分钟,那我播放超过八分钟,就算是正样本,少于八分钟算是负样本。这里完播80%,只是举个例子,你也可以把完播定义为播放超过20%,或者播放超过50%,怎么样定义完播都行。
训练要做二元分类,播放超过80%算是正样本,小于80%算是负样本,做完训练之后,可以用这个二元分类器在线上预估完播率。举个例子,如果模型输出0.73,意思是视频播放超过80%的概率是0.73,预估的播放率会跟点击率等指标一起作为排序的依据。
在实践中,我们不能把预估的完播率直接用到融分公式中,为什么呢?从直觉上说,视频越长,完播率就越低,一个15秒的短视频完播率会很高,但是15分钟的长视频完播率就会比较低了,如果直接用预估的完播率,那么会有利于短视频,而对长视频不公平。
看一下这张图,这是对视频播放的统计,横轴是视频时长,就是视频的长度有多少秒,纵轴是视频完播率。图中的曲线趋势很明显,视频越长,完播率就越低,这跟我们的直觉是符合的,我们用函数$f$拟合蓝色的曲线,函数$f$的变量是视频长度,我们要用函数$f$对预估的完播率做调整,这样可以公平对待长短视频的完播率。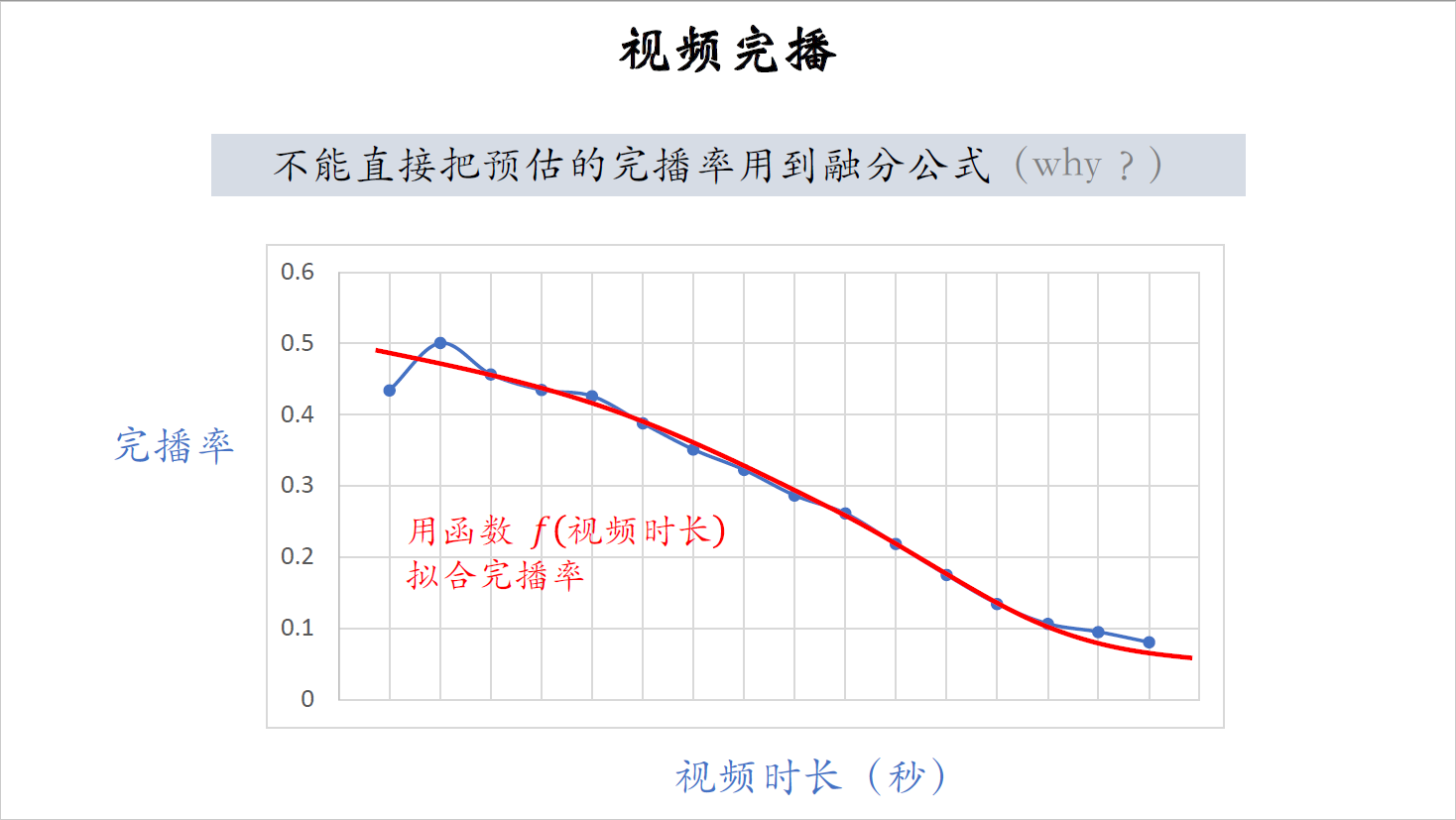
线上预估完播率之后,可以这样对完播率做调整,用预估的完播率除以刚才拟合出的函数$f$。$f$是视频长度的函数,视频越长,函数值$f$越小,把调整之后的分数记作$p_{finish}$,它可以反映出用户对视频的兴趣,而且对长短视频是公平的。把$p_{finish}$作为融分公式中的一项,与播放时长,点击率,点赞率等指标一起决定视频的排序。
这节课我们讨论了视频的排序,视频有两个独特的指标,一个是播放时长,另一个是完播率,我详细解释了如何对播放时长和完播率做建模,这节课就讲到这里,感谢大家观看,
