特征交叉01：Machine（FM）因式分解机

本博文引自王树森老师推荐系统。
视频地址：特征交叉01：Factorized Machine (FM) 因式分解机_哔哩哔哩_bilibili
课件地址： https://github.com/wangshusen/RecommenderSystem

前面的课程介绍了召回和排序模型，这节课后面几节课内容是特征交叉，在召回和排序中都会用到。
这节课介绍最基础的factorized machine，缩写是fm。

几年前fm在召回和排序中都很常用，但是现在fm已经不太常用了，但大家不妨了解一下fm的思想，知道早些年特征交叉是怎么做的。
在讲fm之前，我先讲一下线性模型，设模型用到第一个特征，用$d$维向量$x$表示，用下标表示向量中的元素。这是个线性模型，公式中的$b$是偏移项，英文叫做bias或者intercept，第二项是对$d$个特征的连接，其中的$w_i$表示每个特征的权重，把线性模型的输出记作$p$，它是对目标的预估，为了方便这里我没有用激活函数，如果做二分类，可以用sigmoID激活函数。
这个线性模型有d+1个参数，$w_1$到$w_d$是权重，$b$是偏移项，不难看出，线性模型的预测是特征的加权和，$d$个特征$x_1$到$x_d$只有相加，没有相乘，也就是说特征之间没有交叉。在推荐系统的应用中，特征交叉是很有必要的，可以让模型的预测更准确。

二阶交叉特征

这个公式用到了二阶交叉特征，这两项跟前面一样，就是个简单的线性模型，区别在后面，这里的$x_i$乘以$x_g$是两个特征的交叉，前面的$u_{ij}$是权重。
用特征交叉的话，两个特征不仅仅能相加，还能相乘，这样可以提升模型的表达能力，举个例子，假设特征是房屋的大小，还有周边楼盘每平米的单价，目标是估计房屋的价格，仅仅用房屋的大小和每平米的单价的加权和是估不准房屋价格的，如果做特征交叉，让房屋大小和每平米单价这两个特征相乘，就能把房价估得很准。这就是为什么交叉特征有用，如果有@个特征，那么模型参数量正比于$d^2$，大多数的参数是交叉特征的权重$u$，如果$d$比较小，这样的模型没有问题，但如果$d$很大，那么参数数量就太大了，计算代价会很大，而且容易出现overfitting。

接下来我们讨论如何减少参数数量，我们重点关注交叉特征的权重$u$，可以把所有的权重$u_{ij}$组成矩阵$U$。$u_{ij}$是$U$的第$i$行，第$j$列上的一个元素。
矩阵$U$有$d$行和$d$列，$d$是参数的数量，$U$是个对称矩阵，可以对矩阵$U$做低秩近似，用矩阵$V$乘以$V$转置来近似矩阵$U$，矩阵$V$有d行，跟$U$一样。$V$有$k$列，$k$远小于$d$，$k$是个超参数，由我们自己设置，$k$越大，$V$乘以$V$转置就越接近矩阵$U$。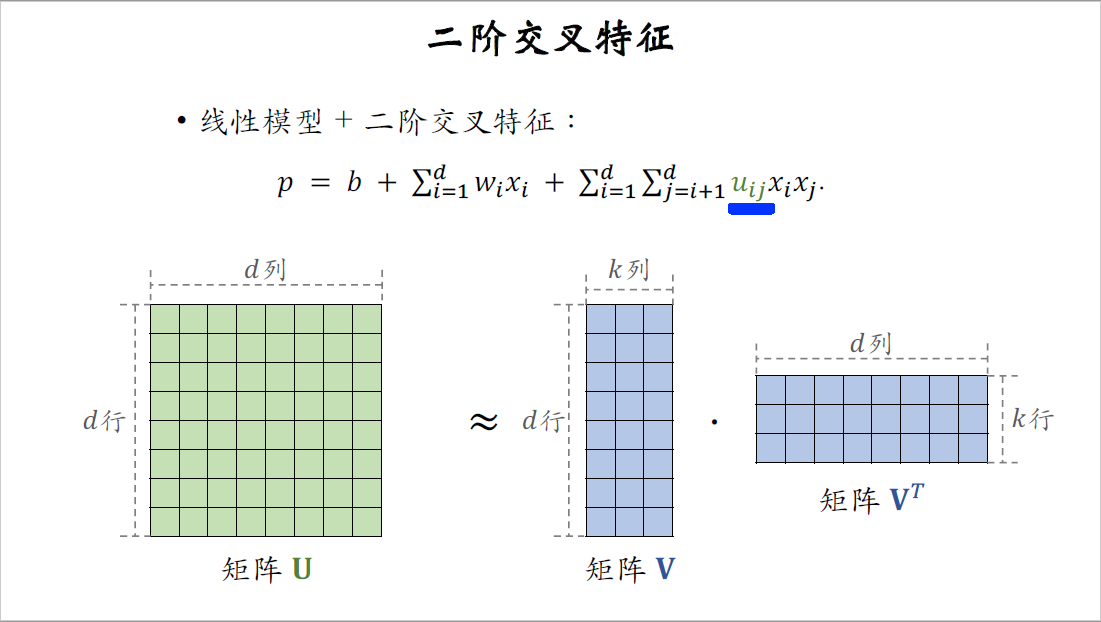

我们看一下权重小$u_{ij}$可以把它近似成$v_i$和$v_j$的内积，我在图中标注一下，$u_{ij}$是矩阵$U$的第$i$行，第$j$列上的元素，$v_i$是矩阵$V$的第$i$行，$v_j$是矩阵$V$的第$j$行，$u_{ij}$约等于这两个向量的内积。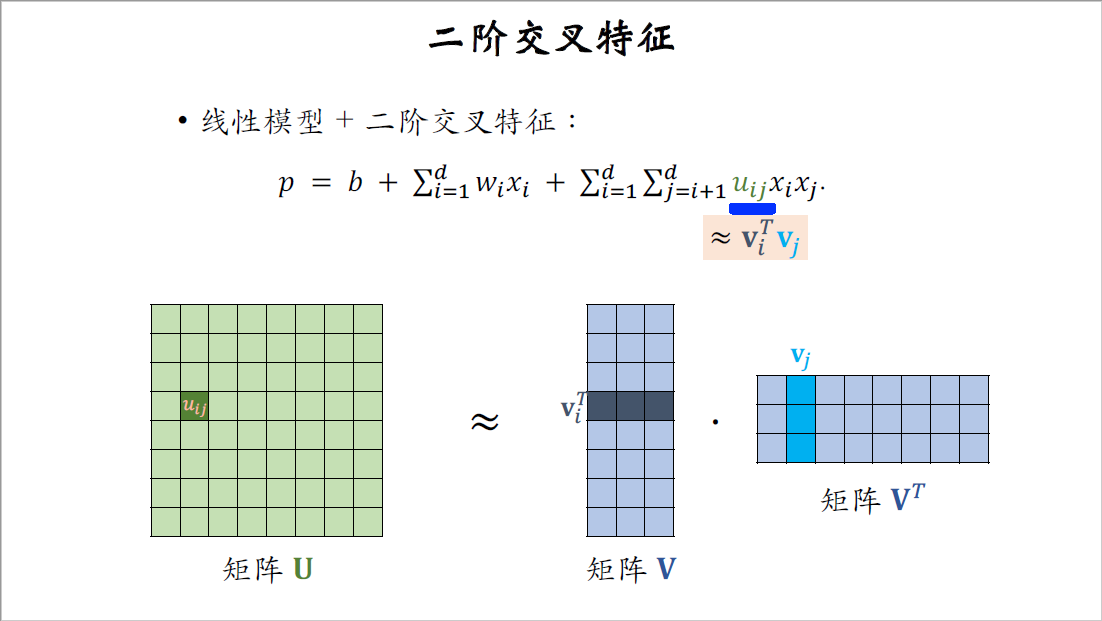

把交叉特征的权重$u_{ij}$近似成向量$v_i$和$v_j$的内积，那么模型就变成了下面的factorized machine。唯一的区别就是在这里，fm用向量$v_i$和$v_j$的内积作为交叉特征的权重，fm的参数数量是矩阵$V$的大小，等于$O(kd)$。$k$是超参数，远比$d$小。
fm的好处在于参数数量更少，从$O(d^2)$降低到了$O(kd)$，这样使得推理的计算量更小，而且不容易出现过拟合。

fm的原理很简单，我已经讲完了，最后总结一下。
fm是线性模型的替代品，凡是能用线性回归，逻辑回归的场景都可以用fm，就是在线性模型后面加上交叉项。fm使用二阶交叉特征，因此模型的表达能力比线性模型更强。尤其是在推荐系统中，交叉特征非常有用，fm的效果显著比线性模型好。
简单粗暴使用二阶交叉特征的话，参数数量是$O(d^2)$，$d$是特征数量。fm的好处在于减少了参数数量，通过把$u_{ij}$近似为向量$v_i$和$v_j$的内积，fm把参数数量从$O(d^2)$降低到了$O(kd)$。
fm是这篇2010年论文提出的，在那个时代，早期的推荐系统通常使用逻辑回归预估点击率，在逻辑回归中用fm做特征交叉，在推荐系统中效果很好，流行了很长一段时间。我的感觉是现在fm在工业界推荐系统中已经过时了，我不清楚其他公司是不是还在用fm，反正我们公司的召回和排序早就下掉了fm。

这节课就讲到这里，感谢大家观看后面的课程，继续讲解各种特征交叉的方法。